в прямоугольном треугольнике АВС (∠С=90°) АВ = 10 см, ∠САВ = 25°. Найти АС и решить а)10/cos25° б)10·cos25° - id1236570220210504 от tambovtsevanat 04.05.2021 05:43

Question

Геометрия: в прямоугольном треугольнике АВС (∠С=90°) АВ = 10 см, ∠САВ = 25°. Найти АС и решить а)10/cos25° б)10·cos25° в)10sin25° г)10 · tg25° 3. в прямоугольном треугольнике АВС (∠С=90°) АС =3см, ВС = 4см. Вычислить sin ∠А 4. Найти синус острого угла а, если cos а = 12/13 5. в прямоугольном треугольнике АВС (∠С=90°) ∠САВ = 30°, ВС =6√3 Найти АВ 6. Установите соответствие между элементами прямоугольных треугольников (1-4) и их значениями(А-Д) (рисунок и задание ниже на картинке) 7. Высота ВД треугольника АВС

tambovtsevanat · Accepted Answer

1)
В прямоугольном треугольнике АВН , АВ равна 13, так как sinA=12/13, тогда по теореме Пифагора АН=√13^2-12^2 = 5

В прямоугольном треугольнике ВНС , ВН/ВС=4/5
12/ВС=4/5
ВС=15
тогда НС=√15^2-12^2= 9

Тогда АС=5+9=14 . По теореме синусов
15/12/13=2R
13*15/24 = R
R=8.125

Длина окружности
L=2*pi*8.125 = 16.25 pi

2) Я вычислил уже стороны они равны 15;14;13
по формуле Герона
p=(15+14+13)/2=21
S=√21*6*7*8 = 84
ответ 84

3) Найдем длину самой биссектрисы
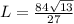
$L=\frac{84\sqrt{13}}{27}\\
$
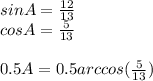
так как $sinA=\frac{12}{13}\\
cosA=\frac{5}{13}\\
\\
0.5A=0.5arccos(\frac{5}{13})\\
\\
$
тогда по теореме косинусов , отрезок первый
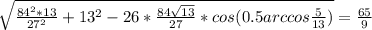
$\sqrt{\frac{84^2*13}{27^2}+13^2-26*\frac{84\sqrt{13}}{27}*cos(0.5arccos\frac{5}{13})}=\frac{65}{9}\\
$
тогда второй
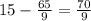
$15-\frac{65}{9}= \frac{70}{9}$

MOGZ ответил