Вокружности с центром o проведены взаимно перпендикулярные хорды pn и nt,pn не равно nt,ob- перпендикуляр к хорде pn,oc-перпендикуляр к хорде nt.укажите верные утверждения1)oc-серединный перпендикуляр к отрезку nt2)ob=oc3)no-бессектриса угла pnt4)pt=2on
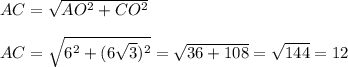
1. Если вписанный угол равен 60°, то центральный (опирающийся на ту же дугу, с вершиной в центре окружности) в 2 раза больше , то есть 120°. Поскольку центральный угол окружности 360°, то есть в 3 раза больше данного, то и длина окружности будет в 3 раза больше данной.⇒ 12х3=36см
4. Радиус описанной ок-ти (R), радиус вписанной ок-ти (r) и половина стороны многоугольника (a/2) образуют прямоугольный треугольник, где R - гипотенуза Δ. По теореме Пифагора найдем а/2 = √(2√3)²-3² =√3 ⇒ а=2√3, то есть сторона многоугольника а равна R это условие выполняется толко в правильном шестиугольнике (центральный угол опирающийся на сторону многогранника равен 60° -из равностороннего Δ со сторонами R,R и а и ⇒360°:60°=6 - сторон).
5. Из предыдущей задачи для правильного шестиугольника R=а. Сторона правильного Δ - b через R определяется по соотношению b=R√3 то есть искомое b=а√3