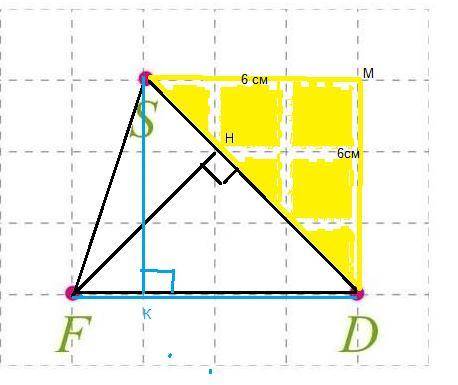
На листочке в клеточку отмечено три точки F, S, D. Известно , что площадь одной клеточки 4 см². Рассчитайте расстояние от F до SD в метрах.
Объяснение:
Расстояние это перпендикуляр. Пусть FH⊥SD. Тогда FH расстояние до SD.
Найдем длину квадрата площадью 4 см² ⇒2*2=4, значит сторона квадрата 2 см.
Пусть SК⊥FD . Найдем площадь ΔFSD
S=1/2*FD*SK , S=1/2*8*6=24 (см²).
С другой стороны S( ΔFSD)=1/2*SD*FH .Нахождение SD внизу.
24=1/2*6√2*FH ⇒FH=  , FH=4√2 см=0,04√2 м
, FH=4√2 см=0,04√2 м
Расстояние от F до SD 0,04√2 м
==================
В желтом прямоугольном треугольнике , со стороной 6 см, по т. Пифагора, SD=√(6²+6²)=√(2*6²)=6√2 ( cм)
Противолежащие стороны параллелограмма равны (из свойства фигуры параллелограмм).
=> BC=AD=12 (см) => BK=12-5=7 (см).
Так как АК - биссектриса (по условию), то она делит угол А так, что углы ВАК и КАD равны между собой.
Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны (из определения).
=> при пересечении двух параллельных прямых секущей накрест лежащие углы равны.
=> угол ВКА = углу КАD, а они накрест лежащие при ВС || АD и секущей АК.
В равнобедренном треугольнике две боковые стороны равны и углы при основании тоже равны (из свойства равнобедренного треугольника).
=> треугольник АВК - равнобедренный (угол ВАК = углу ВКА) и АВ=ВК=7 (см).
Периметр параллелограмма равен удвоенной сумме 2х его соседних сторон (из теоремы о периметре параллелограмма).
=> Р=2*AB+2*AD=2*7+2*12=14+24=38 (см).
ответ: Р параллелограмма АВСD равен 38 (см).