ищем уравнение пряммой ВС
пряммая проходящая через точки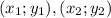 
имеет вид
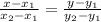
ищем уравнение высоты АД
поэтому уравнение стороны ВС имеет вид
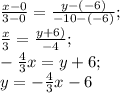
для угловых коэффициентов перпендикулярных пряммых выполянется соотношение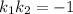 
, поэтому угловой коэффициент прямой, содержащей высоту АД равен
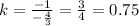
пряммой, содержащей высоту АД, принадлежит точка А, поэтому
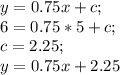
ищем координаты точки Д, как точки пересечения пряммых ВС и АД
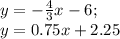
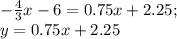
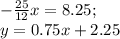
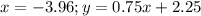
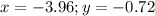
ищем длину высоты АД по формуле расстояния между двумя точками
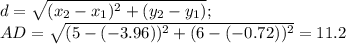
ищем координаты точки М как середины отрезка ВС
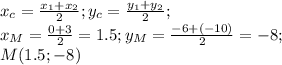
ищем уравнение медианы АМ
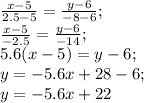
ищем длину стороны АС
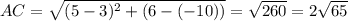
ищем длину стороны ВС
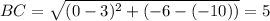
ищем длину стороны АВ
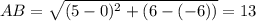
ищем косинус угла В по теореме косинусов
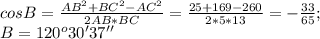
Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, является высотой этой трапеции и делит это основание на отрезки, больший из которых равен полусумме оснований, меньший - их полуразности. ⇒ Средняя линия этой трапеции – 22. Подробное решение: Если опустить еще один перпендикуляр из вершины второго угла при меньшем основании, получим разделенное на 3 части основание, две из которых равны по 15 ( у каждого острого угла при основании), а третья, средняя, равна меньшему основанию и равна
22-15=7.
Длина меньшего основания равна 7,
большего основания равна
22+15=37 .
Сумма длин оснований равна
37+7=44
Средняя линия трапеции равна полусумме оснований и равна
44:2=22