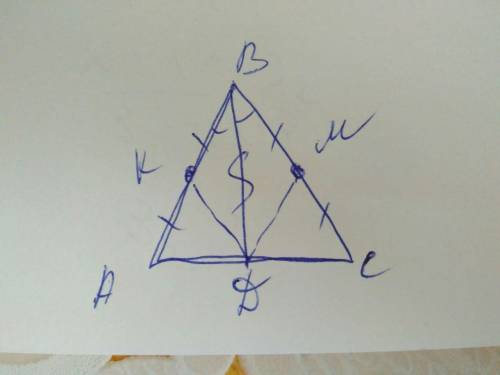
Дано: ΔАВС - равнобедренный, АК = КВ = ВМ = МС (т. К и М - середины боковых сорон АВ и СВ соответственно), ВD - медиана.
Доказать: ΔBKD = ΔBMD.
Доказательство: есть два треугольника BKD и BMD, у которых сторона BD - общая. стороны KB и BM - равны, т.к. ΔABC - равнобедренный, а точки K и M - середины сторон АВ и СВ соответственно. Т.к. BD - медиана равнобедренного ΔABC, то ∠KBD = ∠DBM. Следовательно, по первому признаку равенства треугольников (если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны), треугольники BKD и BMD равны, т.к. KB = BM, BD - общая сторона, ∠KBD = ∠DBM.
Чтд.
√41 см, 2√41 см
Объяснение:
Дано ΔАКО, ∠К=90°, АК=√123. Знайти АО, КО.
Катет, що лежить проти кута 30°, дорівнює половині гіпотенузи. Нехай КО=х см, тоді АО=2х см.
За теоремою Піфагора
(2х)² - х²= (√123)²
4х² - х² = 123
3х²=123
х²=41
х=√41
КО=√41 см, АО=2√41 см