ответ: 13,44 см
Объяснение:
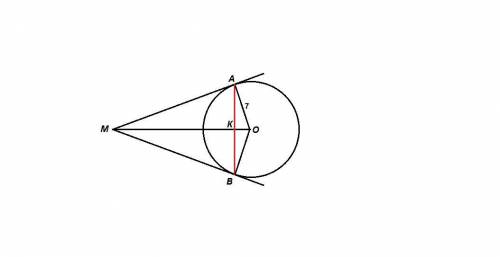
МА и МВ - касательные, точки А и В - точки касания.
MO = 25 см,
ОА = ОВ = 7 см - радиусы.
ОА⊥МА и ОВ⊥МВ как радиусы, проведенные в точку касания.
По свойству касательных, проведенных из одной точки, МА = МВ и ∠АМО = ∠ВМО.
Тогда МК - биссектриса равнобедренного треугольника МАВ, значит является и медианой и высотой, ⇒
К - середина АВ, АК⊥МО.
ΔМОА: ∠МАО = 90°, по теореме Пифагора
МА = √(МО² - ОА²) = √(25² - 7²) = √((25 - 7)(25 + 7)) =
= √(18 · 32) = √(9 · 2 · 16 · 2) = 3 · 2 · 4 = 24 см
АК - высота прямоугольного треугольника МОА.
Smoa = 1/2 MO · AK = 1/2 OA · MA
AK = OA · MA / MO = 7 · 24 / 25 = 168/25 = 6,72 см
АВ = 2 АК = 2 · 6,72 = 13,44 см
Около правильного треугольника описана окружность радиуса R. докажите что R = 2r, где r - радиус окружности, вписанной в этот треугольник.
=============================================================
В правильном треугольнике высоты, медианы и биссектрисы совпадают: АМ = BE = CD. Соответственно, совпадают и центры описанной и вписанной окружности. Центром описанной окружности является точка пересечения серединных перепендикуляров, то есть высоты данного треугольника ⇒ АО = ВО = СО = R . Центром вписанной окружности является точка пересечения биссектрис, то есть биссектрисы данного треугольника ⇒ OE = OM = OD = r.Так как AM = BE = CD - медианы ΔАВС ⇒Медианы треугольника пересекаются и точкой пересечения делятся в отношении 2:1, считая от вершины.Значит, СО:ОD = 2:1 ⇒ R:r = 2:1 ⇒ R = 2r, что и требовалось доказать.