 => 10x+10=60 => 10x=50 => x=5 =>
=> 10x+10=60 => 10x=50 => x=5 =>
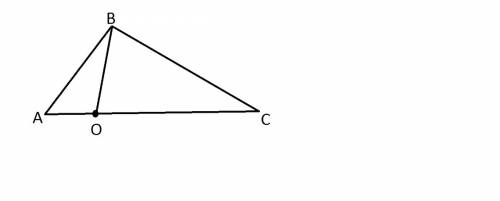
Теорема 1. Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны (рис.2).
Доказательство. Рассмотрим треугольники ABC и A1B1C1, у которых АВ = A1B1, АС = A1C1 ∠ А = ∠ А1 (см. рис.2). Докажем, что Δ ABC = Δ A1B1C1.
Так как ∠ А = ∠ А1, то треугольник ABC можно наложить на треугольник А1В1С1 так, что вершина А совместится с вершиной А1, а стороны АВ и АС наложатся соответственно на лучи А1В1 и A1C1. Поскольку АВ = A1B1, АС = А1С1, то сторона АВ совместится со стороной А1В1 а сторона АС — со стороной А1C1; в частности, совместятся точки В и В1, С и C1. Следовательно, совместятся стороны ВС и В1С1. Итак, треугольники ABC и А1В1С1 полностью совместятся, значит, они равны.
Всего при пересечении двух параллельных прямы секущей образуется 8 углов: 4 угла по 55°, и 4 угла по 180° - 55° = 125°
Пояснение:
Смотри прикреплённый рисунок.
Пусть ∠1 = 55°.
∠3 = ∠1 = 55° (вертикальные углы)
∠5 = ∠ 3 = 55° (внутренние накрест лежащие углы)
∠7 = ∠ 1 = 55° (внешние накрест лежащие углы)
∠2 и ∠ 1 - смежные углы
∠2 = 180° - ∠1 = 180° - 55° = 125°
∠4 = ∠ 2 = 125° (вертикальные углы)
∠6 = ∠4 = 125° (внутренние накрест лежащие углы)
∠8 = ∠ 2 = 125° (внешние накрест лежащие углы)