Объяснение:
Вектор -это направленное перемещение.
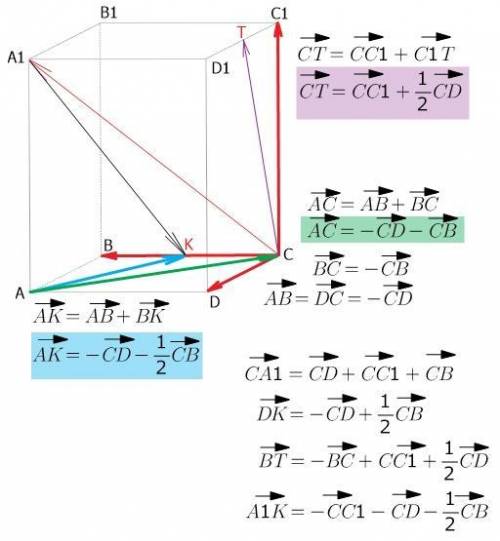
чтобы разложить векторы по указанным векторам, можно представлять, что "как будто вы вышли из вершины А и идете по ребрам призмы в вершину С и записываете свой путь"...
из точки А могу "пройти" в точку В (это вектор АВ); из В могу "пройти" в точку С (это вектор ВС)...
но перемещение из А в В (вектор АВ) по длине в точности равно
перемещению из С в D (вектору CD), только направление в другую сторону... направление "показывает" знак "минус"
вектор АВ = вектору DC
вектор DC = "минус" вектор CD
Задача
В основе прямой призмы лежит равнобедренная трапеция с острым углом 60 и боковой стороной 4 см. Диагонали трапеции являются биссектрисами острых углов. Диагональ призмы наклонена к плоскости основания под углом 45. Найти объем призмы.
Объяснение:
АВСD-трапеция,∠А=∠D=60°, АС-биссектриса ∠А, DВ-биссектриса ∠D, АВ=СD=4 см, ∠ВDВ₁=45°.
Т.к. DВ-биссектриса ∠D, то ∠АDВ=30°,
ΔАВD, ∠А=60° , ∠АDВ=30° ⇒ ∠АВD=90°. Поэтому ΔАВD-прямоугольный : tg60°=ВD/ВА или √3=ВD/4 или ВD=4√3 см
cos60°=ВА/АD или 0,5=4/АD , АD=8 см.
АD║ВС,АD-секущая ⇒ ∠АDВ=∠DВС=30° как накрест лежащие.Поэтому ΔDВС- равнобедренный и СВ=СD=4 см.
ΔВDВ₁-прямоугольный и равнобедренный( ∠ВDВ₁=45° ⇒∠ВВ₁D=45°), поэтому ВВ₁=ВD=4√3 см.
V=P(осн)*h.
V=(4+4+4+8)*4√3 =80√3 ( см³)
62°
Объяснение:
Объяснение в приложении.