Апофемой боковой грани правильной пирамиды называется высота этой грани, проведенная из вершины пирамиды.
Угол между боковой гранью и основанием пирамиды - угол между двумя перпендикулярными лучами, проведенными в плоскости грани и основания к одной точке к линии их пересечения.
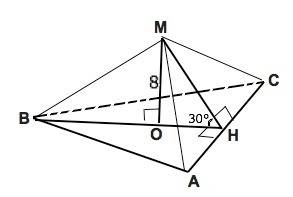
Высота основания АН и высота МН боковой грани пирамиды МАВС перпендикулярны ребру АВ в его середине Н.
Высота пирамиды МО, часть высоты основания ОН и апофема МН образуют прямоугольный треугольник МОН, в котором высота пирамиды – катет, который противолежит углу 30°, а апофема является гипотенузой.
Гипотенуза вдвое больше катета, котороый лежит против угла 30°.
Следовательно, апофема, являясь гипотенузой ∆ МОН, равна 2•8=16 м.
Объяснение:
a — длина
b — ширина
P — периметр
S — площадь
квадрат — определение
P = a + a + a + a; P = a · 4 — периметр квадрата
S = a · a; S = a² — площадь квадрата
прямоугольник — определение
P = a + b + a + b; P = 2a + 2b; P = (a + b) · 2 — периметр прямоугольника
S = a · b — площадь прямоугольника