Знайти площу ромба, сторона якого дорівнює 20 см, а різниця діагоналей дорівнює 8см

Question

Геометрия: Знайти площу ромба, сторона якого дорівнює 20 см, а різниця діагоналей дорівнює 8см​

dergacheva81 · Accepted Answer

1) Боковое ребро образует с плоскостью основания угол 45 градусов следовательно угол АВС(обозначимего так, угол которойнаверху) тоже равен 45 градусов. Следовательно, ВЫСОТА пирамиды=Радиус описанной окружности.

2)Обозначим ВЫСОТУ=РАДИУС ОПИС.ОКР. через х. По т.Пифагора найдем х:

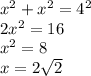
$x^{2}+x^{2}=4^{2}\\ 2x^{2}=16\\ x^{2}=8\\ x=2\sqrt{2}$

ВЫСОТА=РАДИУС.ОПИС.Окр.=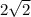 $2\sqrt{2}$

3) Радиус описанной окружности = диагональ квадрата разделить на 2 (В основании квадрат т.к. пирамида 4-х угольная и правильная)

Отсюда, диагональ квадрата = 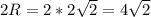$2R=2*2\sqrt{2}=4\sqrt{2}$

4)Сторона квадрата=диагональ кв. делить на корень из 2= 4см

5)Площадь основания = сторона в квадрате=16 см^2

6)бок.поверхн-ть = 1/2 * Периметр основания * высота = 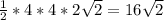$\frac{1}{2} * 4*4*2\sqrt{2}=16\sqrt{2}$

7)Площадь полной поверхности=16+16 кореньиз 2

Знайти площу ромба, сторона якого дорівнює 20 см, а різниця діагоналей дорівнює 8см​

MOGZ ответил