Построение с объяснением ( рисунок прилагается).
Дан угол 45°, который нужно разделить на три равных угла по 45°:3=15°.
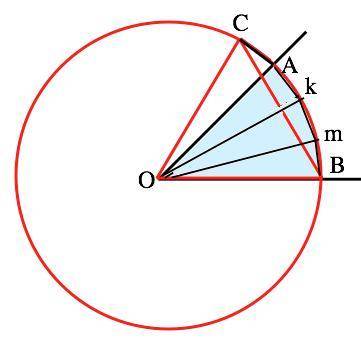
Обозначим вершину угла О. Из т.О, как из центра, проведем окружность. Точки пересечения окружности и сторон угла обозначим А и В.
Циркулем с раствором, равным радиусу АО от т.В сделаем насечку на окружности и отметим т.С . Треугольник СОВ - равносторонний ( все стороны равны радиусу), следовательно, угол СОВ=60°, а угол СОА=60°-45°=15°
Раствором циркуля, равным хорде СА, сделаем насечки на дуге АВ и обозначим их k и m.
Дуги Ak=km=mC, каждая из них стягивается равной хордой и равна 15°, а углы, опирающиеся на равные хорды, равны. АОk=kOm=mOB.
(x/3)^2+y^2=1 - каноническое уравнение эллипса
полуоси 3 (вдоль оси х) и 1 (вдоль оси у)
F1 и F2 - фокусы эллипса, расположены на оси х, так как полуось вдоль х длиннее
фокусное расстояние с=корень(3^2-1^2)=2*корень(2)
F1=(-2*корень(2);0)
F2=(2*корень(2);0)
2)9x^2+25y^2-1=0
(x/(1/3))^2+(y/(1/5))^2=1 - каноническое уравнение эллипса
полуоси 1/3 (вдоль оси х) и 1/5 (вдоль оси у)
F1 и F2 - фокусы эллипса, расположены на оси х, так как полуось вдоль х длиннее
фокусное расстояние с=корень((1/3)^2-(1/5)^2)=4/15=0,2(6)
F1=(-4/15;0)
F2=(4/15;0)