ответ: ∠АСВ = 112°
Объяснение:
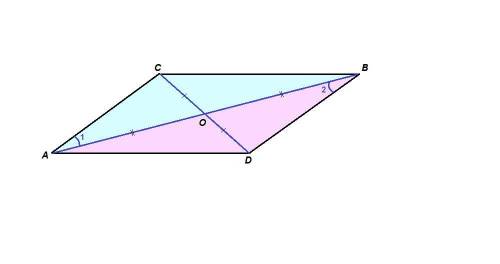
1. АО = ОВ и CO = OD по условию,
∠АОС = ∠BOD как вертикальные, значит
ΔАОС = ΔBOD по двум сторонам и углу между ними.
Из равенства треугольников следует, что
АС = BD и ∠САО = ∠DBO.
2. Тогда в треугольниках АСВ и BDA:
АС = BD, ∠1 = ∠2, AB - общая сторона, значит
ΔАСВ = ΔBDA по двум сторонам и углу между ними.
3. ∠1 = ∠2, а эти углы - накрест лежащие при пересечении прямых АС и BD секущей АВ, значит
АС║BD.
∠АСВ + ∠CBD = 180°, так как эти углы соответственные при пересечении параллельных прямых АС и BD секущей ВС, тогда
∠АСВ = 180° - ∠CBD = 180° - 68° = 112°
Объяснение:
Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
Пусть плоскость проведённая через B, D и серединную точку M ребра B₁C₁ пересекается с плоскостью B₁C₁А₁ по прямой MN. M∈B₁C₁, N∈D₁C₁.
⇒MN||BD⇒BDNM-трапеция
BD||B₁D₁; MN||BD⇒MN||B₁D₁
MN-средняя линия треугольника B₁C₁D₁
ABCDA1B1C1D1- правильный прямоугольный параллелепипед⇒ABCD-квадрат, а боковые грани прямоугольники.
B₁M=0,5B₁C₁=ND₁, DD₁=BB₁, ∠MB₁B=∠ND₁D=90°⇒ΔMB₁B=ΔND₁D⇒MB=ND⇒
⇒BDNM-равнобедренная трапеция. Ч.Т.Д.