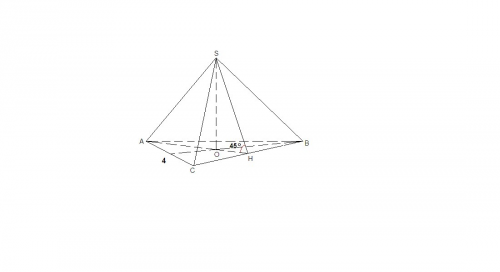
Пирамида правильная, значит в основании правильный треугольник, а боковые грани - равные равнобедренные треугольники.
Пусть Н - середина ВС.
Тогда АН⊥ВС (как медиана правильного треугольника) и SH⊥ВС (так как ΔSBC равнобедренный), тогда
∠SHO = 45° - линейный угол двугранного угла при основании.
ОН = а√3/6 = 4√3/6 = 2√3/3 как радиус вписанной в основание окружности.
ΔSOH равнобедренный прямоугольный, значит SO = OH = 2√3/3
Sabc = a²√3/4 = 16√3/4 = 4√3
V = 1/3 · Sabc · SO = 1/3 · 4√3 · 2√3/3 = 8/3 куб. ед.
Ребра равны, значит вершина пирамиды Д проецируется в точку О пересечение серединных перпендикуляров основания и центр описанной вокруг треугольника окружности. Площадь основания S=(12*18)/2=108. Обозначим в треугольнике АВС АВ=ВС. АС=12. ВК=18 высота основания пирамиды. ДО высота пирамиды=H. По теореме Пифагора АВ= корень квадратный из (ВК квадрат+АК квадрат)=19. По формуле Герона находим площадь основания пирамиды S=корень из 25(25-19)(25-19)(25-12)=108. Радиус описанной окружности R=АО=авс/4S. Где а, в, с стороны треугольника. R=(19*19*12)/4*108=10. Высота пирамиды H=ДО=корень из(АДквадрат-АО квадрат)=24. V=S H/3=108*24/3=864.
1. в 8 раз больше
площадь зависит от радиуса,следовательно 16:2=8
То есть площадь первого шара будет в 8 раз больше второго.
2. 576
Объяснение: