Объяснение:
Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид
{\displaystyle (a+b)^{n}=\sum _{k=0}^{n}{\binom {n}{k}}a^{n-k}b^{k}={n \choose 0}a^{n}+{n \choose 1}a^{n-1}b+\dots +{n \choose k}a^{n-k}b^{k}+\dots +{n \choose n}b^{n}}(a+b)^n = \sum_{k=0}^n \binom{n}{k} a^{n - k} b^k = {n\choose 0}a^n + {n\choose 1}a^{n - 1}b + \dots + {n\choose k}a^{n - k}b^k + \dots + {n\choose n}b^n
где {\displaystyle {n \choose k}={\frac {n!}{k!(n-k)!}}=C_{n}^{k}}{n\choose k}=\frac{n!}{k!(n - k)!}= C_n^k — биномиальные коэффициенты, {\displaystyle n}n — неотрицательное целое число.
В таком виде эта формула была известна ещё индийским и персидским математикам; Ньютон вывел формулу бинома Ньютона для более общего случая, когда показатель степени — произвольное действительное (или даже комплексное) число. В этом случае бином представляет собой бесконечный ряд (см. ниже).
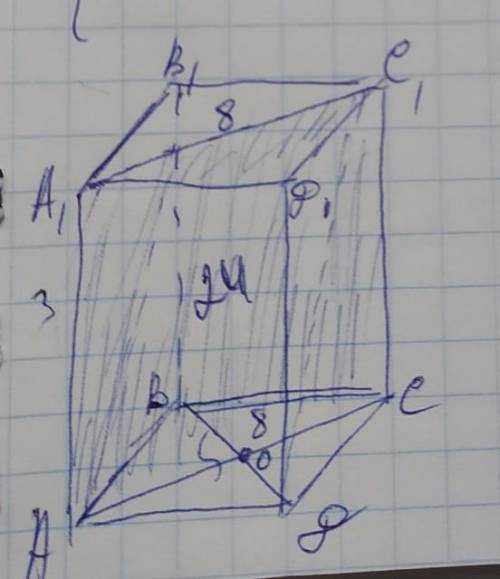
обозначим вершины призмы АВСДА1В1С1Д1 с сечением АА1С1С. Объем призмы вычисляется по формуле: V=Sосн×АА1. Для этого нужно найти площадь основания и высоту призмы. Площадь ромба вычисляется по формуле: Sосн=½×АС×ВД=½×5×8=20см².
Теперь найдём высоту призмы. Сечение призмы представляет собой прямоугольник, одной из сторон которого является искомая высота АА1=СС1 площадь которого 24см², и используя формулу площади найдём высоту: AA1=S÷AC=24÷8=3см
Теперь найдём объем призмы:
V=Sосн×АА1=20×3=60см³
ОТВЕТ: V=60см³
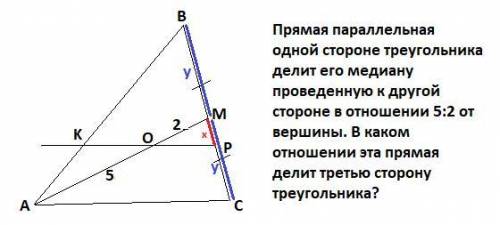
Прямая параллельная одной стороне треугольника делит его медиану проведенную к другой стороне в отношении 5:2 от вершины. В каком отношении эта прямая делит третью сторону треугольника?
Объяснение:
Введем обозначения как показано на чертеже: КР║АС , ВМ=МС=у, МР=х . По условию 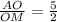 . Необходимо найти
. Необходимо найти 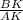 .
.
Т.к. АС║КР , то по т. о пропорциональных отрезках 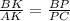 или
или
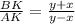 (*) . По т. Менелая для ΔВАМ :
(*) . По т. Менелая для ΔВАМ :
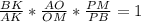 или
или 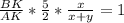 или
или 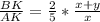 (**).
(**).
Приравняем правые части (*) и (**) : 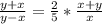 или 2(у-х)=5х или
или 2(у-х)=5х или
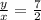 .
.
Вернемся к (**) 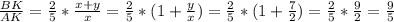 .
.
Надо разложить выражение используя треугольник Паскаля: