1. См. рис.1. Найти отрезок КР. КР = МН – МК – РН.
Т.к. МН – средняя линия трапеции, то МК и РН – средние линии треугольников АВС и ДВС. У этих треугольников общее основание ВС. Следовательно МК = РН = ВС/2 = 8/2 = 4 см. Т.к. МН – средняя линия трапеции , то МН = (АД+ВС)/2 = (16 + 8)/2 = 12 см. Таким образом, КР = 12 -4 -4 = 4 см.
2. См. рис.2. Синие линии нужны для объяснения принципа построения. При построении требуемой прямой их, естественно, не будет.
Внутри угла А поставлена точка М. Через эту точку проведена прямая, пересекающая лучи «а» и «е» в точках С и В соответственно. Если эта линия будет проведена правильно, то в получившемся треугольнике АСВ МА будет медианой, поскольку должно выполниться условие СМ = МВ. Медиана делит площадь треугольника пополам. Т.е. площадь треугольника АВМ должна равняться площади треугольника АМС. Значит, площадь треугольника АВС должна равняться двум площадям треугольника АВМ. Эти треугольники (АВС и АВМ) имеют общее основание АВ. Отсюда следует, что высота РС треугольника АВС должна быть в два раза больше высоты МК треугольника АВМ. Вот это обстоятельство и необходимо использовать при построении. Теперь забыли про синие линии. Их нет.
Из точки М опустим перпендикуляр (МК) на любой из лучей угла, например, на луч «е». Затем проведем прямую параллельно лучу «е» на расстоянии СР = 2МК. Пересечение этой прямой с лучом «а» даст точку С. Проведя прямую через точки М и С построим требуемую линию.
3. См. рис. 3. Требуемое условие будет выполняться, если НК будет параллельна АС. Опять же синяя линия для объяснения принципа. Если НК параллельна АС то треугольники АВД и НВЕ подобны. Так же подобны и треугольники СДВ и КЕВ. Для первой пары подобных треугольников ВД/АД = ВЕ/НЕ. Для второй пары ВД/СД = ВЕ/ЕК. Из этих двух соотношений вытекает, что АД/ДС = НЕ/ЕК. А поскольку АД = ДС, то и НЕ = ЕК. Таким образом, что бы выполнилось требуемое условие НК должен быть параллелен АС.

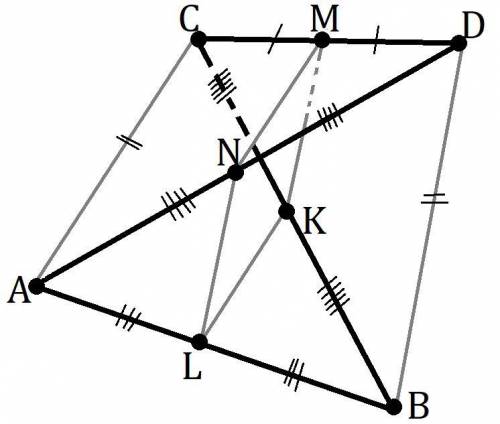
Дано: D∉(ABC); AC=BD; AL=LB (L∈AB); BK=KC (K∈BC); CM=MD (M∈CD); DN=NA (N∈DA).
Доказать: MNLK - ромб.
AC║MN и AC=2MN т.к. MN - средняя линия ΔACD.
AC║LK и AC=2LK т.к. LK - средняя линия ΔACB.
MN║AC║LK ⇒ MN║LK; 2MN=AC=2LK ⇒ MN=LK
MN║LK ⇒ MN, LK ⊂ (MNL), в этой плоскости рассмотрим четырёхугольник MNKL: у него две противоположные стороны параллельны и равны (MN, LK),поэтому это точно параллелограмм у ромба помимо этого ещё все стороны равны, значит чтобы доказать, что MNLK - ромб осталось только доказать, что MK=NM т.к. если это выполняется, то NL=MK - как противоположные стороны параллелограмма, а значит MN=NL=LK=KM.
BD=2MK т.к. MK - средняя линия ΔBDC.
BD=AC - по условию.
2MK=BD=AC=2MN ⇒ MK=MN. Доказали, значит MNLK это параллелограмм у которого все стороны равны, то есть это ромб.
треугольники BAC и DCA равны за двумя сторонами и углом между ними
BA=DC, угол BAC=угол DCA, AC=CA
с равности треугольников следует равенство их углов: угол B=углу D
Доказано