Внутрішній кут правильного многокутника дорівнює 144 градуси.
Знайдіть
А)сторону многокутника , якщо його периметр дорівнює 80 см
напишите как искать полностью

👇

Увидеть ответ

Ответ:

брагим

12.02.2023

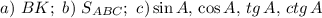
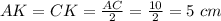
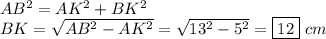
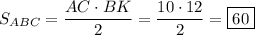
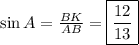
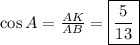
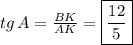
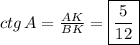
Так как многоугольник - правильный, то все стороны и углы у этого многоугольника равны.

Сначала найдём количество сторон этого многоугольника.

Итак, угол правильного многоугольника вычисляется по формуле :

$a=\frac{180(n-2)}{n}$

Где a - угол правильного многоугольника, n - количество сторон.

Подставим известные значения в формулу и узнаем численное значение переменной n :

$144=\frac{180(n-2)}{n}\\144n = 180(n-2)\\144n = 180n-360\\144n-180n = -360 \\-36n = -360\\n = 10$

Количество сторон = 10.

2) Периметр многоугольника - сумма длин всех сторон.

Можно записать формулу для нахождения периметра правильного многоугольника так :

P=n*d

Где P - периметр, n - количество сторон, d - длина стороны.

Нам нужно найти d :

$80=10d\\d=\frac{80}{10} \\d = 8$

Сторона многоугольника = 8 см.

ответ: 8 см.

4,4(9 оценок)

Открыть все ответы

Ответ:

cucuruza5

12.02.2023

Для определения площади параллелограмма достаточно трёх точек.

Площадь равна модулю векторного произведения векторов АВ и ВС.

Находим векторы ВА и ВС.

ВА = (-3-2; 1-6) = (-5; -5),

ВС = (7--2; -1-6) = (5; -7)

Находим векторное произведение ВА и ВС.

i j k| i j

-5 -5 0| -5 -5

5 -7 0| 5 -7 = 0i + 0j + 35k - 0j - 0i + 25k = 0i + 0j + 60k.

Найдем модуль вектора:

|c| = √(cx² + cy² + cz²) = √(0² + 0² + (-60)²) = √(0 + 0 + 3600) = √3600 = 60

Найдем площадь параллелограмма:

S = 60.

4,4(52 оценок)

Ответ:

глупыйоладушек

12.02.2023

Дано: ABC - равнобедренный треугольник; AB = BC = 13дм, АС = 10см.
Найти: $a)\,\,BK;\,\, b)\,\, S_{ABC};\,\,c)\sin A,\,\cos A,\, tg\, A,\,ctg \,A$
решение:
У равнобедренного треугольника боковые стороны и углы при основания равны
С вершины В проведём перпендикулярно к стороне основанию АС высоту ВК. Делит она сторону на отрезки: $AK = CK = \frac{AC}{2} = \frac{10}{2} =5\,\, cm$
С прямоугольного треугольника ABK ( ∠AKB=90°):
По т. Пифагора высота ВК равна:
$AB^2=AK^2+BK^2 \\ BK= \sqrt{AB^2-AK^2} = \sqrt{13^2-5^2}=\boxed{12}\,\,cm$
Площадь равнобедренного треугольника равна произведению стороны основания на высоту делённое на 2
$S_{ABC}= \dfrac{AC\cdot BK}{2} = \dfrac{10\cdot 12}{2} =\boxed{60}$
Синус угла - это отношение противолежащего катета к гипотенузе:
$\sin A= \frac{BK}{AB} = \boxed{\frac{12}{13}}$
Косинус угла - это отношение прилежащего катета к гипотенузе:
$\cos A= \frac{AK}{AB} = \boxed{\frac{5}{13}}$
Тангенс угла - это отношение противолежащего катета к прилежащему катету
$tg \, A= \frac{BK}{AK} = \boxed{\frac{12}{5}}$
Котангенс угла - это отношение прилежащего катета к противолежащему катету
$ctg \, A= \frac{AK}{BK} = \boxed{\frac{5}{12}}$

Вравнобедренном треугольнике боковая сторона равна 13 дм и основание равно 10 см. найдите: а)высоту