Доказательство в объяснении.
Объяснение:
AE перпендикулярна СК, так как СК перпендикулярна BC (дано), а ВС параллельна AD.
CF перпендикулярна AК, так как АК перпендикулярна АВ (дано), а АВ параллельна СD). Следовательно, точка D - точка пересечения высот треугольника АКС.
В треугольнике АКС высота из вершины К также проходит через точку D, так как все высоты треугольника пересекаются в одной точке.
DM - перпендикулярна АС (дано), а так как из одной точки (D) на прямую (АС) можно опустить единственный перпендикуляр, следовательно точка К, принадлежащая перпендикуляру (высоте) к стороне АС, прохожящему через точку D, лежит на прямой MD, что и требовалось доказать.

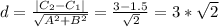
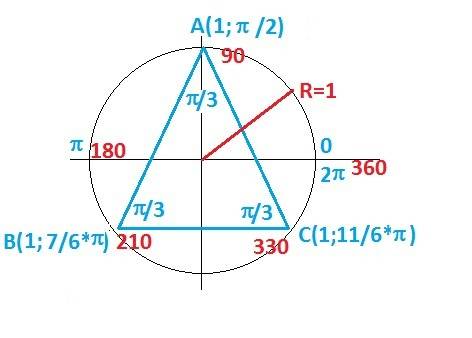
Не знаю, насколько правильно, но все же
Проведём радиусы OB, OA. Они образуют прямые углы с касательной(по свойству). Значит ОВ перпенликулярна ВК, а ОА перпенликулярно АМ.
Также я указала точку F.
Теперь проведём прямые FK и FL, которые будут параллельны прямым OB и OA соответсвенно. Значит, они будут также перпендикулярны к BM и AМ соответственно.
ВО и KF параллельны и OF=FM. Значит по теореме Фаллеса ВК=КМ
Аналогично ОА//FL и OF=FM. Также по т. Фаллеса AL=LM
Теперь рассмотрим треугольники KFM и LFM. Они будут прямоугольными и равнобедренными(углы K, L-прямые, КМ=МF=ML). Значит, углы при катетах будут 45 градусов, а именно углы KMF, KFM, LFM, LMF
Угол АMB состоит из углов KMF и FML. А они по 45. Значит, угол АМВ=45*2=90