ответ: V=64√5см³
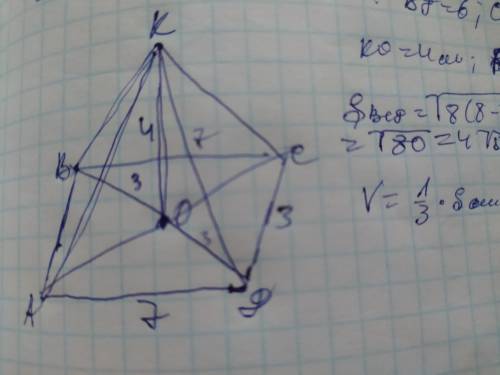
Объяснение: обозначим вершины пирамиды АВСД с высотой КО и диагоналями ВД и АС. Одна диагональ делит параллелограмм на 2 равных треугольника. Пусть ВД=6см. Рассмотрим полученный ∆ВСД. В нём известны 3 стороны и мы можем найти его площадь по формуле: S=√((p-a)(p-b)(p-c)), где а сторона треугольника а р-полупериметр:
Р=3+7+6=16см; р/2=16/2=8см
S=√8((8-7)(8-6)(8-3))=√(8×1×2×5)=
=√80=8√5см²
Так как таких треугольников 2, то площадь параллелограмма=8√5×2=16√5см²
Теперь найдём объем пирамиды зная площадь основания и высоту по формуле: V=⅓×Sосн×КО=
=⅓×16√5×4=64√5/3см³
2. Вспомни теорему Пифагора и опускай перпендикуляры вниз от каждого вектора-отрезка, чтобы потом по этой теореме можно было посчитать их численное значение. Т.е. просто дострой до прямоугольного треугольника каждый вектор другими отрезками (я их карандашом выделил). И посчитай значение каждого вс карандашом) отрезка по клеточкам...
3. Теперь надо по теореме Пифагора считать численное значение каждого основного из трёх векторов-отрезков (которые ручкой), которые будут являться гипотенузами в соответствующих треугольниках.
4. В основном большом треугольнике (ручкой) известны все стороны (основные векторы-отрезки) - по теореме косинусов, используя все стороны этого треугольника, можно найти один из его углов. Пусть это будет угол искомый - между BA и BC.
Посчитав, получил примерно 37,94°. Очень большие числа были, раза 4 проверил всё. И даже транспортиром вручную измерил в конце угол: около 38°. Так что точно правильно.
Если что-то неясно-непонятно, пиши, я всегда на связи.