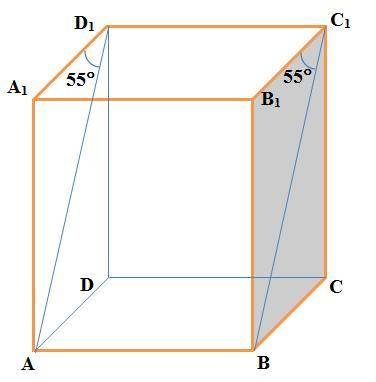
Угол между прямыми C₁B и AA₁ равен 35°
Объяснение:
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).
В задаче C₁B и AA₁ являются скрещивающимися прямыми (см. рисунок). Углом между двумя скрещивающимися прямыми называют угол между двумя пересекающимися прямыми, соответственно, параллельными данным скрещивающимся прямым.
В силу этого, так как C₁B || D₁A, то угол между прямыми C₁B и AA₁ равен углу между прямыми D₁A и AA₁, то есть ∠A₁AD₁. В треугольнике ΔAA₁D₁:
∠AD₁A₁+∠D₁A₁A+∠A₁AD₁=180°.
Тогда, так как ∠AA₁D₁=90° и ∠AD₁A₁=55°, то ∠A₁AD₁=180°–90°–55°=35°.
Отличная задача, я даже не верил, что условие правильное, пока не сообразил :)))
Пусть S - площадь DOEC; S =9;
Если я пишу SAEO, то это площадь треугольника АЕО. Если у треугольников высота общая, то площади относятся как длины оснований, я далее пояснять не буду, почему равны площади, или почему одна в 3 раза больше.
Проведем СО и обозначим SAOE = S1; SCOD = S2; SAOB = S3; (чтобы не таскать кучи букв).
Итак.
SCOE = 3*S2; ( AE:CE= 1:3, последний раз объясняю :));
SODB = S1;
3*(S2 + S3) = (3*S2 + S1 + S1); S3 = (2/3)*S1;
Поэтому АО = (2/3)*ОD;
Обозначим теперь для краткости записи x = AE; y = OD; q = sin(угол DAC)/2; (будьте предельно внимательны, что именно и как я обозначил)
SAOE = S2 = x*(2*y/3)*q; (произведение сторон на синус угла между ними, и пополам, понятно?)
SADC = (4*x)*(5*y/3)*q; = S + SAOE;
(4*x)*(5*y/3)*q - x*(2*y/3)*q = S; y*x*q = S/6; (ура!)
SADC = SABC/2 = (20/3)*y*x*q = (20/3)*(S/6) = (20/18)*S;
SABC = S*20/9 = 20;