Шеңбердің екі нүктесі оны бұрыштық шамалары 8:12 қатынасындай болатын екі доғаға бөледі. Егер шеңбердің радиусы 8-см ге тең болса, осы доғалардың ұзындықтарын табу керек.
Чтобы найти координаты вектора XY для точек X(x1,x2,x3) и Y(y1,y2,y3) нужно переместить X в 0, т.е просто отнять x1 из y1 и т.д. Итого XY(y1-x1, y2-x2, y3-x3). Аналогично вычисляем:
AB(1-2,-2-4,3-5)=AB(-1,-6,-2)
BC(-1-1,-2-(-2),4-3)=BC(-2,0,1)
AC(-1-2,-2-4,4-5)=AC(-3,-6,1)
Вектор XY*k получается домножением каждой координаты на k, чтобы вычесть вектора нужно из координат первого вектора вычесть координаты второго вектора:
Построим сумму векторов а и b и их разность. ↑АС = ↑р = ↑а + ↑b ↑DB = ↑q = ↑a - ↑b Чтобы найти угол между векторами p и q, построим вектор, равный вектору q, с началом в точке А. ∠ЕАС - искомый. Из ΔABD найдем длину вектора q по теореме косинусов: |↑q|² = AB² + AD² - 2·AB·AD·cos60° = 25 + 64 - 2·5·8·1/2 = 89 - 40 = 49 |↑q| = 7 Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°, значит ∠АВС = 120°. Из ΔABС найдем длину вектора р по теореме косинусов: |↑p|² = AB² + BC² - 2·AB·BC·cos120° = 25 + 64 + 2·5·8·1/2 = 89 + 40 = 129 |↑p| = √129
Из ΔЕАС по теореме косинусов: cos α = (AE² + AC² - EC²) / (2 · AE · AC) cos α = (49 + 129 - 256) / (2 · 7 · √129) = - 78 / (14√129) = - 39√129 / 903 cos α = - 13√129/301
а)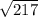
б)-28
Объяснение:
Чтобы найти координаты вектора XY для точек X(x1,x2,x3) и Y(y1,y2,y3) нужно переместить X в 0, т.е просто отнять x1 из y1 и т.д. Итого XY(y1-x1, y2-x2, y3-x3). Аналогично вычисляем:
AB(1-2,-2-4,3-5)=AB(-1,-6,-2)
BC(-1-1,-2-(-2),4-3)=BC(-2,0,1)
AC(-1-2,-2-4,4-5)=AC(-3,-6,1)
Вектор XY*k получается домножением каждой координаты на k, чтобы вычесть вектора нужно из координат первого вектора вычесть координаты второго вектора:
a=3AB-4AC=(3*(-1)-4*(-3),3*(-6)-4*(-6),3*(-2)-4*1)=(9,6,-10)
Длина вектора a - среднее квадратичное его координат:
|a|=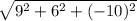 =
=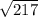
Формула скалярного произведения векторов a(a1,a2,a3) и b(b1,b2,b3) - ab=a1*b1+a2*b2+a3*c3
Итого ab=9*(-2)+6*0+(-10)*1=-28