Длина МА находится по Пифагору.
Объяснение
Наклонная МА - это гипотенуза прямоугольного треугольника ADM с прямым углом МDA (дано). По Пифагору МА = √(AD²+DM²).
AD - cторона квадрата АВСD, равна √S (S - площадь). Тогда
а) МА = √(21+100) = √121 =11 см.
б) МА = √(96+100) = 196 = 14 см.
в) МА = √(44+100) =√144 = 12 см.
г) МА = √(69+100) = √169 = 13 см.
д) МА = √(156+100) = √256 = 16 см.
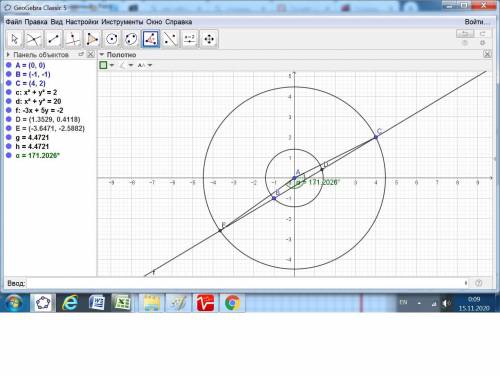
В задании, очевидно, надо определить ПЛОЩАДЬ закрашенной фигуры.
Она представляет собой разность сегментов двух заданных кругов.
Радиусы их равны:
АВ = √((-1)² + (-1)²) = √2,
АС = √(4² + 2²) = √20.
Площадь сегмента круга находится, как разность площади сектора AOB и площади равнобедренного треугольника AOB, выраженную через угол.
Sсегм = (R² /2)(πα° /180° −sin(α°)).
Находим координаты точек пересечения окружностей с заданной прямой решением систем из уравнения окружности и прямой.
Точка Е: x² + y² = 20, 3x - 5y - 2 = 0. E(-62/17; -44/17).
Точка D: x² + y² = 2, 3x - 5y - 2 = 0. D(23/17; 7/17).
Площади сегментов равны:
Площадь Площадь
28.3511 2.1810
ответ: S = 28.3511 - 2.1810 = 26,1701 .
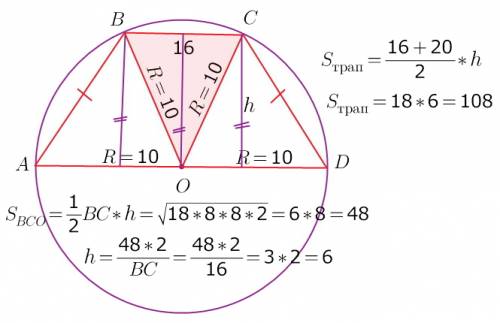
точкаД- основание перпендикуляра, АД=√S, ∆AMD -прямоугольный, МА=√(S+10²)=
а) =11см, б) =14см, в) =12см, г) =13см, д) =16см