МР = √41; МЕ = √34
Объяснение:
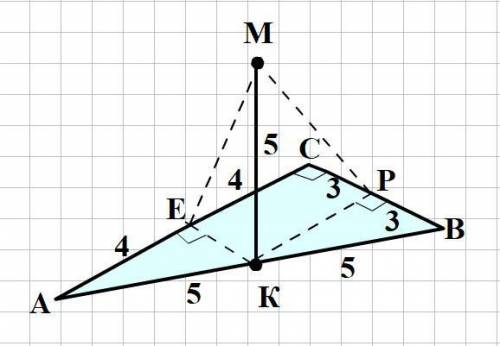
Смотри рисунок на прикреплённом фото.
Найдём гипотенузу АВ = √(АС² + ВС²) = √(8² + 6²) = 10
Из точки К проведём перпендикуляры КР и КЕ соответственно к сторонам ВС и АС. КР и КЕ являются средними линиями в ΔАВС.
КР = 0,5АС = 4; КЕ = 0,5ВС = 3.
Проведём наклонные МР и МЕ, которые и являются расстояниями от точки М до прямых ВС и АС, так как по теореме о 3-х перпендикулярах ВС ⊥ КР ⇒ ВС ⊥ МР и АС ⊥КЕ ⇒ АС ⊥МЕ.
Найдём МР и МЕ по теореме Пифагора.
МР = √(КР² + КМ²) = √(4² + 5²) = √41
МЕ = √(КЕ² + КМ²) = √(3² + 5²) = √34
ответ: P=124,1 см.
Объяснение:
Первая сторона=34,7 см.
Вторая сторона=на 17,8 см больше первой, и на 15,6 см больше третьей.
Третья сторона=на 15,6 см меньше второй стороны.
P=? см.
1) 34,7+17,8=52,5 (см) — длина второй стороны.
2) 52,5-15,6=36,9 (см) — длина третьей стороны.
3) 34,7+52,5+36,9=124,1 (см) — периметр треугольника.
ответ: P=124,1 см.