Будем использовать следующие значения для сторон треугольника АВС: АВ=с, ВС=а, СА=b и его углов:
<А=а, <В=b, <C=y (a, b, y : Альфа, Бэта, Гама.)
Дано:
а=4, b=5, c=6.
Найти: a, b, y -?
Пусть b - наибольшая сторона, b<a+c.
По теореме косинусов находим наибольший угол b,
[Не обязательно писать, для ориентира: Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними.]
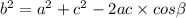
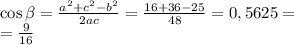
При основного тригонометрического тождества найдём Sin B
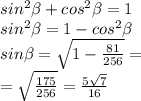
С теоремы синусов найдём углы треугольника:
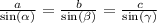
Отсюда,
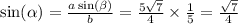
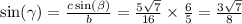
С таблиц находим градусную меру углов:
а≈41°
b≈57°
Тогда,
у≈82°
ответ: 41° 57° 82°
∠А+∠В+∠С=180
50+х+12х=180
13х=130°, х=10°
∠В=10°, ∠С=120°
2) ∠С=90° , ∠В=35°, ∠А=90°-35°=55°
ΔАСD, ∠D=90°, ∠ACD=35°
3) ΔABC, ∠A=∠B - 60°, ∠C=2*∠A,
∠A=x, ∠B=x+60, ∠C=2x
x+(x+60)+2x=180
4x=180-60=120
x=120÷4
x=30
∠A=30°, ∠B=30°+60°=90°, ∠C=30°*2=60°
4) Высота разбивает равнобедр. треугольник на 2 прямоугольных треугольника. Высота является в полученном треугольнике - катетом и она в 2 раза меньше боковой стороны т.е. гипотенузы, поэтому катет лежит против угла 30°. Значит углы при основании равнобедренного треугольника по 30°,
а угол при вершине 180°-30°-30°=120°
ответ: наибольший угол при вершине равнобедренного треугольника.