Конус.
L = РА = 5 (м).
∠РАО = 30°.
Найти:V - ? (м³).
Решение:V = (1/3)πR²h
Осевое сечение этого конуса (если ось плоскость проходит через ось конуса) - равнобедренный треугольник, а высота ВН делит этот равнобедренный треугольник на два равных прямоугольных △АРО и △ВРО (их равенство можно доказать по всем признакам равенства прямоугольных треугольников, исходя из того, что △АРВ - равнобедренный)
Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.
⇒ РО = Н = 5/2 = 2,5 (м).
Найдём радиусы АО и ВО, по теореме Пифагора: (с² = а² + b², где с - гипотенуза, а, b - катеты).
b = √(c² - a²) = √(5² - 2,5²) = √(25 - (5/2)²) = √(25 - 25/4) = √75/4 = √75/2 = 5√3/2 (м).
Итак, АО = ВО = 5√3/2 (м).
V = π((5√3/2)² ⋅ 2,5 ⋅ 1/3) = π(25/4 ⋅ 5/2 ⋅ 1/3) = 125/8π = 15,625π (м³).
ответ: 15,625π (м³).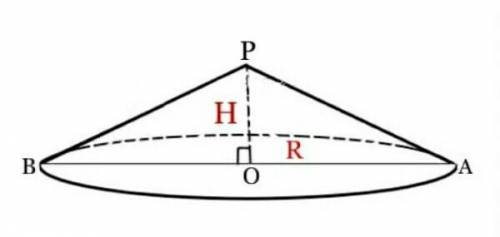
ответ: 54
Объяснение: 1) S трапеции =1/2*h*(BC+AD)
=>S трапеции ABCD=1/2*h*(6+12)=1/2*h*18=9*h
2) Проведем высоту из вершины С. Тогда трапеция поделится на прямоугольник ABCH(т.к все углы =90 градусов) и треугольник CHD. Рассмотрим треугольник CHD. В нем:
угол CDH=45
угол CHD=90
=> угол HCD=45(тк сумма углов в треугольнике =180 градусов)
Тк два угла равны, то треугольник равнобедренный (по признаку равнобедренного треугольника)=>HD=CH
Тк BCHD - прямоугольник, то BC=AH=6(по свойству параллелограмма (а любой прямоугольник - это параллелограмм)
HD=AD-AH=12-6=6
=>CH=HD=6
Значит, высота трапеции = 6
Значит, S трапеции ABCD=9*6=54 см
Старалась максимально подробно, рисунок в прикрепленном файле