ответ:S=16π
Объяснение:в основании образуется треугольник, состоящий из двух радиусов, к-ые относятся к дуге с 60°, и сторонной, полученной сечением квадрата. Сторону квадрата находим по Пифагору: √(a²+a²) = 4√2, a = 4. Основание треугольника так же равно 4. Этот треугольник, в первую очередь, является равнобедренным, так как имеет две равных сторон (радиусов окружности), но по той причине, что вершина равна 60, это правильный треугольник. Следовательно, все его стороны равны, что указывает, что радиусы равны 4. Зная радиус, мы можем найти длину окружности: 2πr=4π. Высотой цилиндра является сторона квадрата, т.к. второй пересекает его параллельно оси. Отсюда S=4π*4=16π
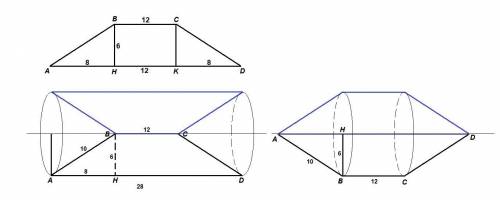
Равнобокая трапеция с основаниями 12 см и 28 см и высотой 6 см в первый раз вращается около меньшего основания, а во второй - около большего. Сравните площади поверхностей полученных тел вращения.
S₁ > S₂
Объяснение:
Найдем боковую сторону трапеции.
Проведем высоты ВН и СК. ВНКС - прямоугольник, так как все углы прямые, значит
НК = ВС = 12 см
ΔАВН = ΔDKC по гипотенузе и катету (АВ = CD, т.к. трапеция равнобедренная, ВН = СК как высоты), ⇒
АН = DK = (AD - HK) / 2 = (28 - 12) / 2 = 8 см
Из прямоугольного ΔАВН по теореме Пифагора:
АВ = √(АН² + ВН²) = √(64 + 36) = 10 см
1.
При вращении трапеции около меньшего основания получается цилиндр с двумя одинаковыми коническими выемками.
Для цилиндра:
Н = 28 см - высота,
R = 6 см - радиус основания.
Для конуса:
l = 10 см - образующая,
r = 6 см - радиус основания.
Площадь поверхности тела вращения:
S₁ = Sбок. цилиндра + 2· Sбок. конуса
S₁ = 2πRH + 2 · πrl = 2π · 6 · 28 + 2π · 6 · 10 = 336π + 120π = 456π см²
2.
При вращении трапеции вокруг большего основания, получается цилиндр с двумя одинаковыми конусами, имеющими с цилиндром общие основания.
Для цилиндра:
R = 6 см - радиус основания,
Н = 12 см - высота.
Для конуса:
r = 6 см - радиус основания,
l = 10 см - образующая.
Площадь поверхности тела вращения:
S₂ = Sбок. цилиндра + 2· Sбок. конуса
S₂ = 2πRH + 2 · πrl = 2π · 6 · 12 + 2π · 6 · 10 = 144π + 120π = 264π см²
S₁ > S₂
угол ВОД=2*BND=2*68=136