ответ
Пусть длина диагонали ВД = 4 * Х, тогда диагональ АС = 7 * Х см.
Диагонали параллелограмма, в точке их пересечения, делятся пополам, тогда ОВ = ВД / 2 = 2 * Х см.
В треугольнике АВС отрезок ВО есть его медиана, так как точка О делит АС пополам.
По формуле медианы треугольника:
ВО2 = (2 * АВ2 + 2 * ВС2 – АС2) / 4.
4 * Х2 = (98 + 162 – 49 * Х2) / 4.
16 * Х2 + 49 * Х2 = 260.
Х2 = 260 / 65 = 4.
Х = 2.
ВД = 2 * 4 = 8 см, АД = 2 * 7 = 14 см.
ответ: Диагонали параллелограмма равны 8 см и 14 см.
Объяснение дай лучший ответ
Доказательство:
Так как треугольник остроугольный и BD - биссектриса, то ∠B<90°⇒∠CBD<45°=∠DFC, следовательно F∈BC.
Проведем из точки D перпендикуляр до отрезка BC с основанием M, M будет принадлежать стороне BC поскольку треугольник остроугольный.
Тогда прямоугольные треугольники BDE и BDM равны по общей гипотенузе BD и острым углам ∠DBE, ∠DBM. Из этого следует что,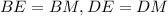 .
.
Также из-за того что, ∠DBC<∠DFC=45°<∠DMC=90°⇒F∈BM, теперь можно пользоваться тем что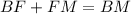 .
.
Заметим что, DFM - прямоугольный треугольник с углом 45°, то есть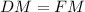 .
.
Учитывая доказанные равенства получаем,
Что требовалось доказать.