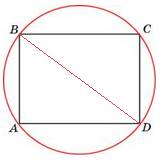
1) Если прямоугольник вписан в окружность, то его диагональ - диаметр этой окр-сти, тогда ВD= 2*R=2*5=10.
2)Пусть АВ =а, ВС =b, тогда по теореме Пифагора а^2+b^2=BD^2
а^2+b^2=100
C другой стороны: a*b= 48. Решим систему ур-ий:
{ а^2+b^2=100
a*b= 48 I *2 и сложим уравнения
{ а^2+b^2=100
2* a*b= 48 *2
______________
а^2+b^2+ 2* a*b =196
(a+b)^2= 14^2
a+b= 14
P = 2*(a+b) =2*14=28
ответ : 28.
Последовательно вычитаем из 180 21 и ли 49 и находим больший угол.
2) В правильном многоугольнике углы и стороны равны. В правильном многоугольнике, вписанном в окружность углы лежат на окружности, следовательно отрезки соединяющие углы с центром окружности будут радиусы. Все проведенные радиусы к углам правильного многоугольника, деля его на равнобедренные треугольники, одновременно деля углы пополам. Следовательно углы при основании этих треугольников будут равны 70 гр. Следовательно углы при вершине этих треугольников будут равны 180-70-70=40 гр. Их общая сумма равна 360 гр. Отсюда 360:40=9 сторон.