1.
Синус угла A — равен: AB/CB.
Так как угол нам уже известен(42°), то его синус найдём по таблице: 0,6691.
Тоесть — катет CB равен: 0.6691*8 = 5.353.
Катет AC — найдём по теореме Пифагора: 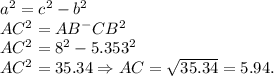
Вывод: AC = 5.94; CB = 5.353.
2.
Второй катет равен(по теореме Пифагора):
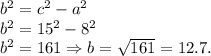
Второй катет равен: 12.7.
Найдём углы по их тангенсам.
Тангенс угла А равен: противоположный катет делить на прилежащий катет.
У нас есть треугольник ABC(прямой угол — C), по нашим расчётам — AB = 15; AC = 8; BC = 12.7.
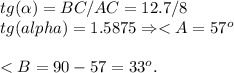
Вывод: <B = 33°; <A = 57°.
3.
<M = 70° => <K = 90-70 = 20°.
Формула вычисления катета, зная гипотенузу, и угол прилежащего катета таков:
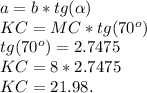
Гипотенузу найдём по теореме Пифагора:
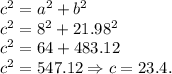
1)Через вершину С провести прямую параллельно диагонали.
Получится треугольник АСЕ,
в котором АЕ = 14+1=15м, АС = 13м, СЕ = 14м.
Найти площадь этого треугольника по формуле Герона.
Потом найти высоту этого треугольника, разделив две его площади на АЕ, то есть на 15.
Высота эта будет и высотой трапеции, площадь трапеции можно найти по формуле: S=1/2(a+b)h
2)Разность осн-ний=13см.
Высоты отсекают от большего осн-ния отрезки, один из кот. =х, другой=(13-х)
Выразив высоту трапеции через диагональ и часть большего осн-ния, получаем:
169-x^2=196-(13-x)^2
Найти "х", вычислить высоту (h)
Найти площадь по ф-ле: S=h*(a+b)/2=?