Question

Знайдіть площу рівнобічної трапеції, основи якої дорівнюють 10 см і
8 см, а діагоналі перпендикулярні до бічних сторін

Answer 1

ответ:27см²

Объяснение:во вложении

Answer 2

OA =OD =  OB  =OC   = Знайдіть площу рівнобічної трапеції, основи якої дорівнюють 10 см і   8 см, а діагоналі перпендикулярні до бічних сторін .

Дано:                                         рисунок  во вложении

ABCD  равнобедренная трапеция

AD || BC ;  

AB = CD ;

AD = 10 см ;

BC = 8 cм ;

∠ACD = ∠DBA =90° .

______________

S - ?

S = ( (AD +BC) /2 )  *h , нужно вычислить только высоту  трапеции

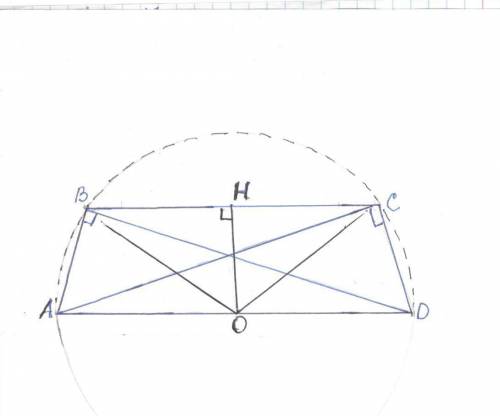
Около  равнобедренной  трапеции    можно омисать  окружность (сумма противоположных углов  равна  180°) . В данной  задаче  центром  окружности  является  середина  большого  основания  AD поскольку ∠ACD = ∠DBA =90° .  

R=  AD /2 = 10 /2  см =5 cм    

OA  = OD = OB = OC = R =5 cм  

Высоту  трапеции нетрудно  определить  из  равнобедренного треугольника OBC .  Проведем  OH ⊥ BC , BH =CH =BC/2 =4 см ;

h = OH

Из ΔOHB по теореме Пифагоа    OH =√(OB² - BH²) =√(5² - 4²) = 3 (см)

S = 0,5*(10+8)*3 = 9*3 = 27 (см²)

ответ: 27 см².