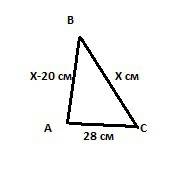
Построим треугольник соответствующий условиям:
АС=28 см.
Угол В=60°
ВС на 20 см больше АВ.
Тогда пусть сторона ВС будет равна х сантиметров, а сторона АВ х-20 см.
По теорем косинусов:
АС²=BC²+AB²-2*BC*AB*cos B
28²=x²+(x-20)²-2*x*(x-20)*cos 60°
784=x²+x²-40x+400-2(x²-20x)*0.5
784= x²+x²-40x+400-x²+20x
784=x²-20х+400
Решим полученное уравнение:
x²-20x+400-784=0
x²-20x-384=0
D=(-20)²-4*1*(-384)
D=1936
x₁=(20-√1936)/2*1=-12
x₂=(20+√1936)/2*1=32
Так как сторона не может быть меньше 0:
ВС=32 см
АВ=32-20=12 см
Периметр равен:
P=28+32+12=72 см.
1) Найдем радиус окружности, впсинной в треуг. МКР
r=S/p, где S - площать треуг. МКР, а р - полупериметр этого треуг.
Площадь треугольника найдем по формуле Герона
S=корень из (р (р-МК) (р-МР) (р-КР) )
p=(4+5+7)/2=8 cm
S=корень из (8(8-4)(8-5)(8-7))=корень из (8*4*3*1)=4 корня из 6.
r=(4 корня из 6) / 8 = (корень из 6) / 2.
2) Найдем радиус сферы по теореме Пифагора
R=корень из (r^2+h^2), где h - расстояние от центра сферы до центра окружности, вписанной в треугольник.
R=корень из (3+5)=корень из 8.
3) Объем сферы V=(4/3)pi*R^3
V=(4/3)pi*8 корней из 8 = (32/3)pi* корней из 8