Объём правильной четырёхугольной пирамиды равен 160, площадь основания равна 16. Найди боковое ребро пирамиды.
Ребро правильного тетраэдра равно 19 м. Вычисли площадь полной поверхности.
Основанием пирамиды является ромб, сторона которого равна 4 см и острый угол равен 30°.
Все углы, которые образуют боковые грани с плоскостью основания, равны 60°.
Вычисли высоту и площадь боковой поверхности пирамиды.
Пирамида пересечена плоскостью, параллельной основанию,
которая делит высоту пирамиды в отношении 2 : 5, считая от вершины.
Вычисли площадь основания, если площадь сечения равна 8 дм2.
 с прямым углом
с прямым углом  , EF — биссектриса
, EF — биссектриса  ,
,  , FG — искомый отрезок.
, FG — искомый отрезок.  .
.  — биссектриса, то
— биссектриса, то  (биссектриса
(биссектриса  делит
делит  на два равные угла).
на два равные угла). 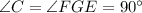 (это следует из условия: так как
(это следует из условия: так как  прямоугольный, то и
прямоугольный, то и  ; так как
; так как  — расстояние от
— расстояние от  до
до 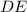 , то
, то 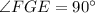 ).
).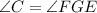 и
и 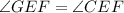 , то и третий угол первого треугольника равен третьему углу второго треугольника:
, то и третий угол первого треугольника равен третьему углу второго треугольника:  . Это следует из того факта, что сумма углов любого треугольника равна 180°. Тогда можно записать так:
. Это следует из того факта, что сумма углов любого треугольника равна 180°. Тогда можно записать так: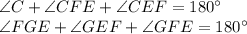
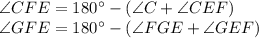
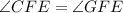 .
.  является для обоих треугольников общей.
является для обоих треугольников общей. (второй признак равенства треугольников — по стороне и двум прилежащим к ней углам (
(второй признак равенства треугольников — по стороне и двум прилежащим к ней углам ( — сторона, а
— сторона, а  — два прилежащих угла)).
— два прилежащих угла)). соответствует
соответствует  , тогда:
, тогда: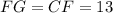
 . Смотрите второй рисунок.
. Смотрите второй рисунок.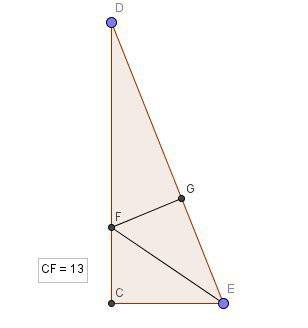
1
17
Пошаговое объяснение:
Объём пирамиды:
где Н -высота пирамиды, S- площадь основания.
Высота пирамиды, половина диагонали основания - как катеты и боковое ребро - как гипотенуза образуют прямоугольный треугольник.
Обозначим половину диагонали как а, тогда квадрат бокового ребра равен:
Н²+а².
Найдем а.
Т.к. пирамида - правильная, то в основании лежит квадрат. Значит его сторона равна √16=4. А диагональ такого квадрата равна: √(4²+4²)=√32.
Значит а=√32/2
Найдем Н из формулы объёма пирамиды.
Тогда квадрат бокового ребра равен:
Н²+а² = 3² + 32/4 = 9+8 = 17.
2
S=361√3 см^2
Объяснение:
правильный тетраэдр - правильный многогранник, все грани которого правильные треугольники.
S полн пов=4×Sправильного треугольника.
площадь. правильного треугольника:
=> площадь полной поверхности:
= а во 2 степени умножить на корень 3
= 19 во 2 степени умножить на корень 3 = 361 корень 3
3
Если все двугранные углы при основании равны 60°, то проекция высоты боковой грани на основание - это радиус вписанной в основание окружности, равный половине высоты h ромба.
h = a*sin30° = 4*(1/2) = 16 см, тогда h/2 = 16/2 = 8 см.
Находим высоту боковой грани:
hгр = (h/2)/cos 60° = 8/(1/2) = 16 см.
Площадь боковой поверхности равна:
Sбок = (1/2)*Р*hгр = (1/2)*(4*32)*16 = 1024 см².
Высота пирамиды равна:
H = (h/2)*tg 60° = 8√3 см.
4