5) Периметр квадрата со стороной AM равен 4AM.
4AM=2BC <=> AM=BC/2
Отрезок из прямого угла к гипотенузе, равный ее половине - медиана.
AM - медиана и высота, следовательно △ABC - равнобедренный, острые углы 45.
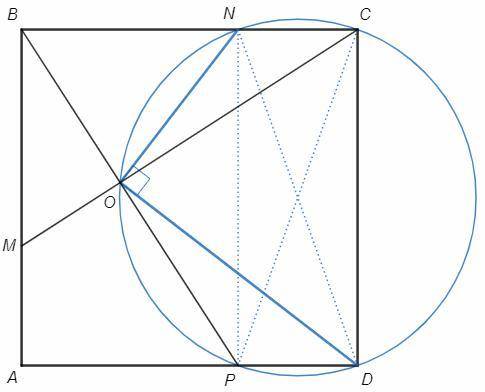
6) Продолжим перпендикуляр BO до пересечения с AD в точке P.
OBM= 90-OMB =BCM
△ABP=△BCM (по катету и острому углу)
AP=BM=BN => PD=NC
PNCD - прямоугольник, диагонали являются диаметрами описанной окружности.
COP=90, точка O лежит на окружности с диаметром CP.
Вписанный угол NOD опирается на диаметр ND, NOD=90
| (угол) - 2х
|| (угол) - 3х
||| (угол) - 4х
2х+3х+4х=180°
9х=180°
х=20°
| (угол) = 2 * 20 = 40°
|| (угол) = 3 * 20 = 60°
||| (угол) = 4 * 20 = 80°