Объяснение:
1
<В=23 градуса
<С=90 градусов
<А=90-<В=90-23=67 градуса
2
<ВНС=90 градусов, т. к ВН - высота, тогда
<СВН=90-<ВСН=90-54=36 градусов
3
Углы равностороннего тр-ка равны:
180:3=60 градусов
4
<B=180-(A+<C)=180-(50+35)=95 градусов
<ВМН=180-(<В+<ВНМ)=180-(95+35)=50 градусов
<НМА=180-<ВМН=180-50=130 градусов т. к смежные
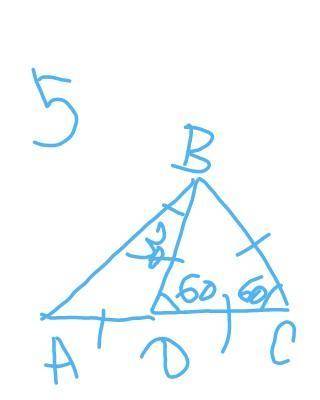
5
Тр-к ВDC - равнобедренный, т. к <С=<ВDC=
=60 градусов
<СВD=180-(<C+<BDC)=180-(60+60)=60 градусов, значит тр-кВDC-равносторонний
ВD=DC=BC
<ADB=180-<BDC=180-60=120 гродусов
Тр-к АВD:
<А=180-(АDB+ABD)=
=180-(120+30)=30 градусов, значит тр-к равнобедренный :
АD=BD, a BD=BC, значит АD=BC
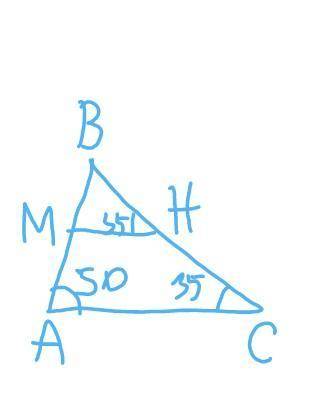
Значит, РС+AD=2·15
РС+25=30
РС=5
ВС=ВР+РС
25=ВР+5
ВР=25-5=20
∠PAD=∠BPA - внутренние накрест лежащие при параллельных ВС и AD и секущей АР.
∠ВАР=∠РАD - биссектриса АР делит угол А пополам.
Значит ∠BPA =∠ВАР и треугольник АВР - равнобедренный АВ=ВР=20
Противоположные стороны параллелограмма равны CD=AB=20
Из треугольника АСD по теореме косинусов:
АС²=AD²+DC²-2·AD·DC·cos ∠D
(5√46)²=25²+20²-2·25·20·cos ∠D
1150=625+400-1000·cos ∠D
cos ∠D =-0,125
Противоположные углы параллелограмма равны
∠В=∠D
Из треугольника АBP по теореме косинусов:
АP²=AB²+BP²-2·AB·BP·cos ∠B
АP²=20²+20²-2·20·20·(-0,125)
АP²=400+400+100
АP²=900
AP=30
Р( трапеции АРСD)= АР+РС+СD+AD=30+5+20+25=80
ответ. Р=80