CH = 3√2
AB = √2
угол BAC = 45
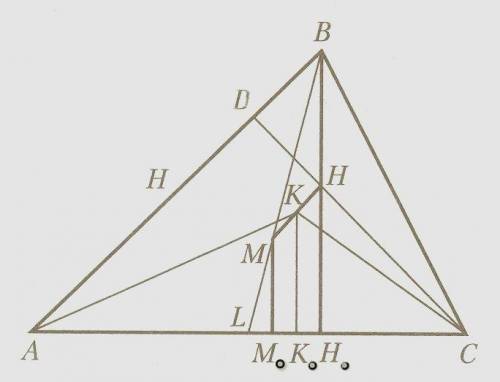
CD - высота, BL - медиана
Из точек M, K, H опустим перпендикуляры на сторону AC
В треугольнике ADC: угол ADC = 90⁰, угол DAC = угол DCA = 45⁰ (следует из условия угол BAC=45⁰)
В треугольнике HH₀C: угол HH₀C = 90⁰, угол H₀CH = угол H₀HC = 45⁰, HH₀ = CH₀ = CH*Sin45⁰ = 3
В треугольнике BH0A: AH₀ = BH₀ = AB*Sin45⁰ = 1
Трегольники BH₀L и MM₀L подобны, тогда из свойств медиан треугольника MM₀ = BH₀/3 = 1/3 (точка пересечения медиан делит их в отношении 2 к 1)
КК₀ - средняя линия трапеции MHH₀M, т.е. KK₀ = (MM₀ + HH₀)/2 = 5/3
AC = AH₀ + H₀C = 4
площадь треугольника AKC = AC*KK₀/2 = 10/3
По св-ву р/б тр. углы при основании равны =а
2а+120=180
2а=60
а=30
по св-ву в прямоугольном треугольнике катет (она же высота) лежащий напротив угла в 30 градусов =1/2 гипотенузы =1/2*с где с -боковая сторона
тогда площадь треугольника равна=1/2*h*a=1/2*1/2*c*36=9c
но площадь треугольника также равна =1/2b*b*sin120=1/2b^2*sqrt(3)/2
1/2c^2*sqrt(3)/2=9c
c=36/sqrt(3)