В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой. Доказательство.Обратимся к рисунку, на котором АВС — равнобедренный треугольник с основанием ВС, АD — его биссектриса.Из равенства треугольников АВD и АСD (по 2 признаку равенства треугольников:AD-общая;углы 1 и 2 равны т.к. AD-биссектриса;AB=AC,т.к. треугольник равнобедренный) следует, что ВD = DC и 3 = 4. Равенство ВD = DC означает, что точка D — середина стороны ВС и поэтому АD — медиана треугольника АВС. Так как углы 3 и 4 смежные и равны друг другу, то они прямые. Следовательно, отрезок АО является также высотой треугольника АВС. Теорема доказана. В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой Если в треугольнике два угла равны, то он равнобедренный. Если в треугольнике медиана является и высотой, то такой треугольник равнобедренный.
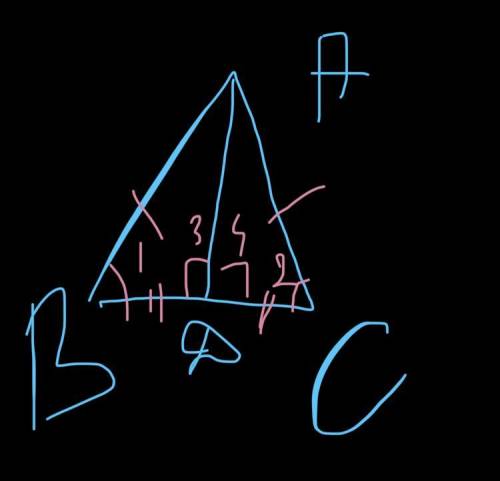
В равнобедренном треугольнике медианы, проведенные к боковым сторонам, равны.
Доказательство: Пусть ABC - равнобедренный треугольник (AC = BC), AK и BL - его медианы. Тогда треугольники AKB и ALB равны по второму признаку равенства треугольников. У них сторона AB общая, стороны AL и BK равны как половины боковых сторон равнобедренного треугольника, а углы LAB и KBA равны как углы при основании равнобедренного треугольника. Так как треугольники равны, их стороны AK и LB равны. Но AK и LB - медианы равнобедренного треугольника, проведённые к его боковым сторонам.
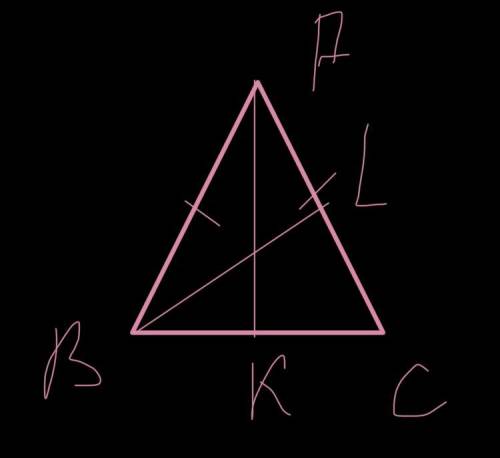
1) Выясним вид четырёхугольника АВСD.
СС1 - перпендикуляр к плю(АВС), С1D- наклонная к этой плоскости,
DC - проекция наклонной СС1 на пл.(АВС).
По условию АD ⊥ DC1, тогда AD ⊥DC (теорема о 3-х перпенд.),
значит АВСD - прямоугольник, а учитывая, что <СAD=45' . то АВСD -квадрат.
Таким образом, ABCDA1B1C1D1 - прав. призма.
2) S бок = Р осн * Н
3)Из Δ ACD- прям.: СD = AC/√2 = 8/√2=4√2,
Р осн = 4·4√2 =16√2
S бок = Р осн * Н= 16√2·4√2 =128.