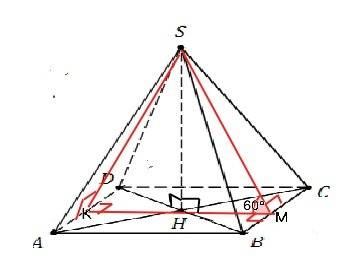
В основании правильной пирамиды - правильный многоугольник (здесь - квадрат), вершина высоты проецируется в его центр. Величина двугранного угла при ребре основания - угол между апофемой и прямой, проведенной через основание высоты параллельно одной из сторон ( обе перпендикулярны ребру в одной точке). Осевое сечение этой пирамиды - правильный треугольник ( углы при основании равны 60°), поэтому сторона основания равна основанию этого правильного треугольника. АВ=КМ=SM=10 см Ѕ(ABCD)=10²=100 см²
Sкруга=пR^2
R=AO=AC/2.
Рассмотрим треуг. АСД: угол Д=90 градусов, АД=СД=
По т. Пифагора найдем АС:
АО=АС/2=
Получается,
ответ: 54п.