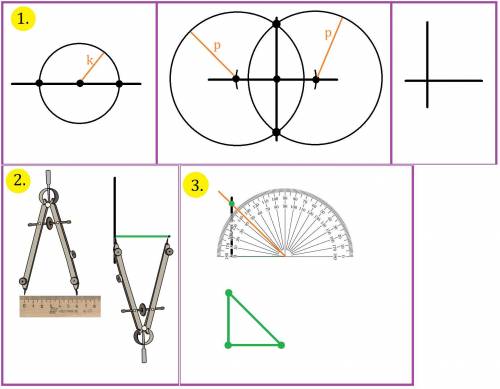
Проведём 2 перпендикулярные прямые (см. рис. 1). Для этого:
1. Из точки на произвольной прямой, проведём окружность произвольного радиуса k.
2. В точках пересечения окружности с прямой, проведём окружности с радиусом p, при это p > k.
3. Через точки пересечений окружностей проводим прямую, она будет перпендикулярна первой прямой.
С циркуля замерим на линейке 6 см и отложим 6 см на одной стороне прямого угла (см. рис. 2).
С транспортира отложим угол в 45° и соединим точки, как показано на рис. 3. Получили искомый треугольник.
Из точки О построим перпендикуляры ОК, ОН, ОК к прямым АВ, ВС и АС.
Треугольники ОВК и ОВН прямоугольные и равны, так как гипотенуза ОВ у них общая, а угол ОВН = ОВК, так как ВО биссектриса, тогда ОК = ОН.
Аналогично треугольник ОСН = ОСМ, а тогда ОМ = ОН.
Следовательно ОК = ОН = ОК, а значит через точки К, Н, С можно провести окружность с центром в точке О.
Треугольники АКО и АМО прямоугольные, у которых ОК = ОМ как радиусы окружности, АО общая гипотенуза, тогда треугольники равна по катету и гипотенузе. Следовательно, угол КАО = МАО, а АО биссектриса угла ВКМ и ВАС, что и требовалось доказать.