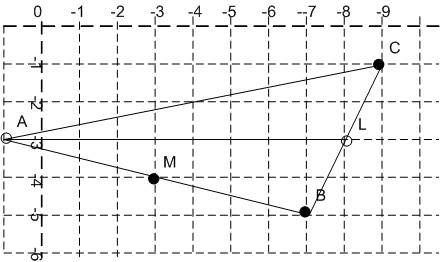
Первое решение - геометрическое.
Строим на тетрадном листике координаты и чертим точки с известными координатами. Так как нам известно, что точи М и L - середины отрезка, то доводим линию BM до точки A и видим, что он оказывается в координатах A(1,-3). Также по чертежу видно, что координаты L(-8.-3). По чертежу выйдет, что AL - прямая линия и ее длина составляет 9 клеток.
Решение по формулам
У нас есть B и С - точка середины отрезка L вычисляется по формуле
L = (B+C)/2.
Lx = (-7 + -9)/2 = -8; Ly= (-5 + -1) / 2 = - 3.
Координаты L(-8.-3).
Если подумать, то отрезок AB с точкой M - тоже вычисляется по этой же формуле:
M = (A + B) / 2.
Отсюда A = 2M - B
Значит
Ax = (2 * (-3)) - (-7) = +1
Ay = (2 * (-4)) - (-5) = - 3
Точка A(1,-3)
Длина отрезка AL = квадратный корень из ((Ax - Lx) ^2 + (Ay - Ly)^2))
AL =квадраткорень( (1- (-8))*(1- (-8)) + (-3- (-3))* (-3- (-3)) = квадраткорень (9*9 - 0*0) = 9
Как-то так.
1.Вертикальные углы — это пары углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого.
Вертикальными называются два угла, стороны одного из которых являются дополнительными лучами до сторон другого угла.
Вертикальные углы равны.
При пересечении двух прямых образуются две пары вертикальных углов
2.Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны
3.Равнобедренный треугольник (isosceles triangle)— это треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона — основанием.
4.В равнобедренном треугольнике углы при основании равны
В равнобедренном треугольнике с основанием ВС проведем биссектрису АДТреугольники АВД=АСД по 1 признаку равенства т к АВ=АС по условию,АД-общая сторона <BAD=<DAC т к АД-биссектриса
В равных треугольниках против равных сторон лежат равные углы,поэтому <B=<C
5.Медиа́на треуго́льника (лат. mediāna — средняя) ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Иногда медианой называют также прямую, содержащую этот отрезок