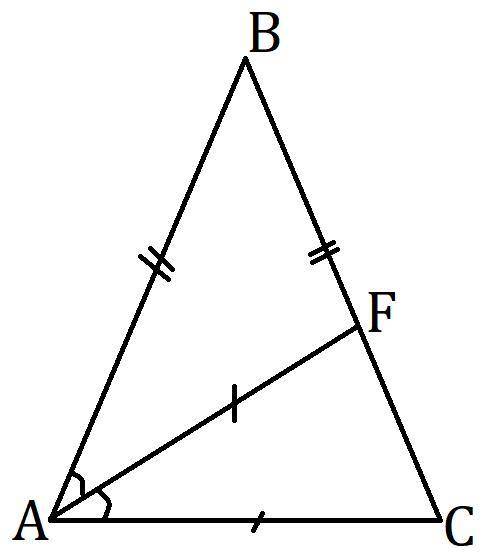
Найти: ∠ABC, ∠BCA, ∠BAC - ?
Пусть ∠BAC = 2x.
В равнобедренном треугольника углы при основании равны.Тогда ∠BCA = ∠BAC = 2x.
Биссектриса делит угол на два равных.Поэтому ∠BAF = ∠CAF = ∠BAC:2 = x.
ΔAFC - равнобедренный т.к. AF=AC.
∠AFC = ∠ACF = 2x, как углы при основании.
Сумма углов треугольника равна 180°.В ΔAFC:
∠AFC+∠ACF+∠CAF = 180°;
2x+2x+x = 180°;
5x = 180°;
2x = 180°:5·2 = 72°.
∠BCA = ∠BAC = 2x = 72°;
В ΔABC:
∠ABC+∠BCA+∠BAC = 180°;
∠ABC = 180°-72°-72°;
∠ABC = 36°.
ответ: 36°, 72° и 72°.
1.
Пусть ∠1=х°, тогда ∠2=(42+х)°, что в сумме составляет 180° по определению смежных углов. Составим уравнение:
х+42+х=180; 2х=138; х=69.
∠1=∠3=69°; ∠2=∠4=69+42=111°.
2. Дано: ∠ВМК и ∠АМК - смежные, МС - биссектриса ∠АМК. Найти ∠СМК и ∠СМВ.
Пусть ∠ВМК=х°, тогда ∠АМК=5х°, что в сумме составляет 180°.
х+5х=180; 6х=180; х=30.
∠ВМК=30°, ∠АМК=30*5=150°
∠СМК=1/2 ∠АМК = 150:2=75°
∠СМВ=∠СМК+∠ВМК=75+30=105°
3. Дано: АВ и СD - прямые, ∠СОК=118°, ОК - биссектриса ∠АОD. Найти ∠ВОD.
∠КОD и ∠СОК - смежные, значит, их сумма составляет 180°.
∠КОD = 180-118=62°
∠АОК=∠КОD=62° (по определению биссектрисы)
∠АОК+∠КОD=62+62=124°
∠ВОD=180-124=56°