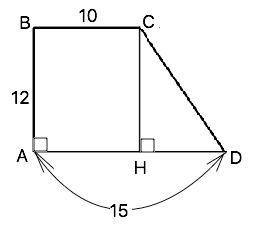
В трапеции ABCD основания AD и BC равны 15см и 10см соответственно, угол А = 90°, АВ = 12 см. Найдите периметр трапеции.
ответ: 50 см
Объяснение:
Периметр многоугольника - сумма длин всех его сторон. Известны три стороны трапеции, следует найти боковую сторону СD.
Опустим высоту СН. Треугольник СНD - прямоугольный с катетами СН и НD и гипотенузой СD.
АВСН - прямоугольник ( АН||ВС, СН||АВ, АВ и СН перпендикулярны основаниям).
СН=АВ=12.
АН=ВС=10
НD=АD-АН=15-10=5 (см)
По т.Пифагора СD=√(CH²+HD²)=13 см
P=AB+BC+CD+AD=12+10+13+15=50 см
Сначало найдём ∠А:
Сумма острых углов прямоугольного треугольника равна 90°
∠А = 90 - 60 = 30°
Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.
=> СВ = 1/2АВ
Пусть х - СВ, тогда 2х - АВ.
Их сумма равна 9 см
х + 2х = 9
3х = 9
х = 3
3 см - СВ
3*2 = 6 см - АВ
ответ: 3 см.