1-а
2-б
3-г
4-г
так как треугольник равнобедренный, то от периметра отнимаем основание 17-5=12 и делим на два, так как боковые стороны равны 12÷2=6 см
5-б так как сумма углов в треугольнике равна 180°, то от 180°-72°=108° сумма двух других углов
6-б так как 6-2=4
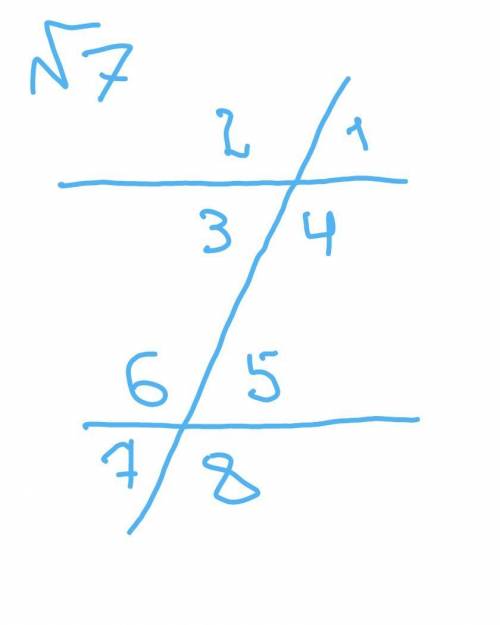
7-пусть угол 1=78°
угол 1=угол 3=78° как вертикальные
угол 3=угол 5=78° как накрест лежащие
угол 5=угол 7=78° как вертикальные
угол 2=180°-78°=102° так как угол 1 и 2 смежные
остальные находятся аналогично
угол 2=угол 4=угол 6=угол 8=102°
8-Пусть 1 часть - это х. На основание приходится 3 части, на боковые стороны по 4 части. Составим уравнение: сложим части и прировняем к 88:
3х+4х+4х=88
11х=88
х=88÷11
х=8 см
Так как х=2, то основание равно 3х=3×8=24 смя, а боковые стороны 4х=4×8=32 см
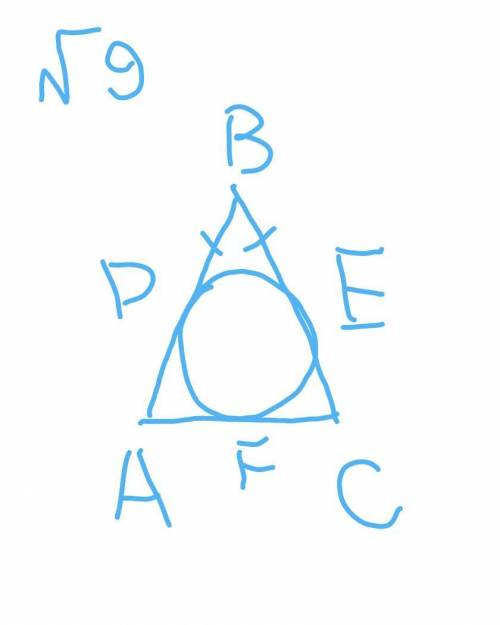
9-Пусть х — длина одной части отрезка, тогда:
Т.к. треугольник равнобедренный, то CE = AD = 2x, BE = BD = 3x.
CE = CF = 2х и AF = AD = 2х как отрезки касательных, проведенные из одной точки.
P = AB + BC + AC = AD + DB + BE + CE + AF + FC = 2x + 3x + 3x + 2x + 2x + 2x = 14x
14x = 70
x = 5 (см)
BC = BK + CK = 2x + 3x = 5x = 5*5 = 25 (см)
ответ: 25 см.
Отметь мой ответ лучшим
Я старался)
РА=РВ=РС=6 см
1. Рассмотрим Δ АОР - прямоугольный.
АО²+РО²=РА² - (по теореме Пифагора)
АО = √(РА²-РО²) = √(6² - (√13)²) = √(36-13) = √23 (см)
2. АО является радиусом описанной окружности.
R=(a√3) / 3
a= (3R) / √3 = (3√23)/√3 = √69 (см) - это длина стороны основы.
3. Находим периметр основы.
Р=3а
Р=3√69 см
4. Проводим РМ - апофему и находим ее.
Рассмотрим Δ АМР - прямоугольный.
АМ=0,5АВ=0,5√69 см
АМ²+РМ²=РА² - (по теореме Пифагора)
РМ = √(РА²-АМ²) = √(6² - (0,5√69)²) = √(36-17,25) = √18,75 = 2,5√3 (см)
5. Находим площадь боковой поверхности пирамиды.
Р = 1/2 Р₀l
Р = 1/2 · 3√69 · 2,5√3 = 3,75√207 = 3,75·3√23 = 11,25√23 (см²)
ответ. 11,25 √23 см².