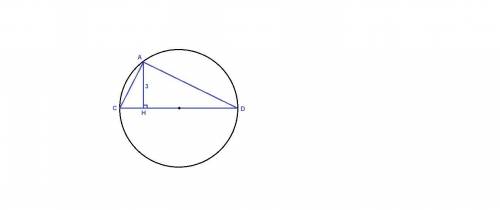
Неточность в вопросе: точка А удалена от прямой CD на расстояние, равное 3 см.
Sacd = 6√3 см²R = 2√3 смОбъяснение:
∠DАС вписанный, опирается на полуокружность, значит
∠DАС = 90°.
АС - катет, равен половине гипотенузы, значит лежит против угла в 30°:
∠ADC = 30°.
ΔAHD: ∠АНD = 90°, ∠ADH = 30°, ⇒ AD = 2AH = 2 · 3 = 6 см
Обозначим радиус окружности R. Тогда CD = 2R, AC = CD/2 = R/
По теореме Пифагора из треугольника ACD:
AC² + AD² = CD²
R² + 36 = 4R²
3R² = 36
R² = 12
R = 2√3 см
AC = 2√3 см,
Sacd = 1/2 AC · AD = 1/2 · 2√3 · 6 = 6√3 см²
Решение (1 вариант):
Вертикальные углы равны.
∠AOD и ∠ВОС - вертикальные.
=> ∠AOD = ∠BOC.
Так как ВО и ОС - радиусы => ВО = ОС.
=> ∆ВОС - равнобедренный.
180 - 74 = 106° - сумма ∠В и С.
Так как ∠В = ∠С (по свойству равнобедренного треугольника) => ∠В = ∠С = 106 ÷ 2 = 53°
(Угол С это АСВ)
ответ: 53°.
Решение (2 вариант):
угол АОВ+угол АОD=180˚, так как они смежные => угол АОВ=106˚.
угол АСВ=53°, как вписанный, опирающийся на ту же дугу, что и центральный угол AOB.
ответ: 53°.