Если 3 точки лежат на одной прямой, то тангенсы угла наклона соединяющих их прямых равны.
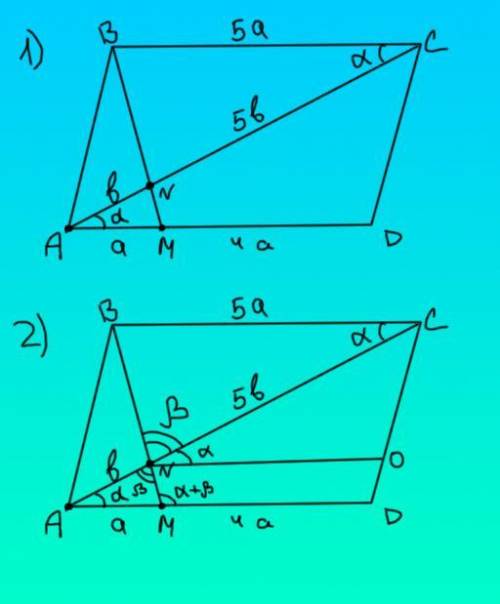
1) Пусть AM = a, AN = b. Тогда по условию NC = 5b, а MD = 4a, BC = 5a. Пусть угол NAM = α. Т.к AC - диагональ, то и угол BCA = углу NAM = α, ведь диагональ пересекает два параллельных основания. Треугольники AMN и BCN подобны по углу и прилегающим к нему сторонам.
2) Пусть угол BNC = β, тогда из подобия ANM тоже = β. Проведем прямую NO, которая параллельна BC и AD. Угол СNO будет равен α, т.к это угол при двух параллельных прямых и секущей. А угол BNO будет равен α + β. Угол DMN является внешним для треугольника ANM, он равен сумме внутренних не смежных с ним углов. DMN = α + β. Т.к. NO ║ AD и тангенсы угла наклона прямых BN, NM и BM равны, то точки B, M, N лежат на одной прямой, чтд
отмечаем на прямой а точку А. От нее откладываем длину данного катета. Пересечение прямой и отложнного катета является точка В. Циркулем делаем засечку на данном угле. ОТ точки В откладываем замеренную засечку. На данном углезамеряем расстояние между концами угла, где засечка и откладываем ее на рисунке. это мы сделали данный нам угол (угол В)и прямую в. Затем нам надо построить прямой угол А. Ставим кончик циркуля на точку А и откладываем произвольный отрезок вправо и влево. Замеряем расстояние между пересечениями засечек с прямой а. И из каждого пересечения откладываем данную замерку. Пересечение этих замерок мы соединяем с точкой А. Мы получили прямой угол (угол А) и прямую с. Пересечение прямой в и с является точка С. Соединяем точки А,В,С и получаем искомый треугольник АВС