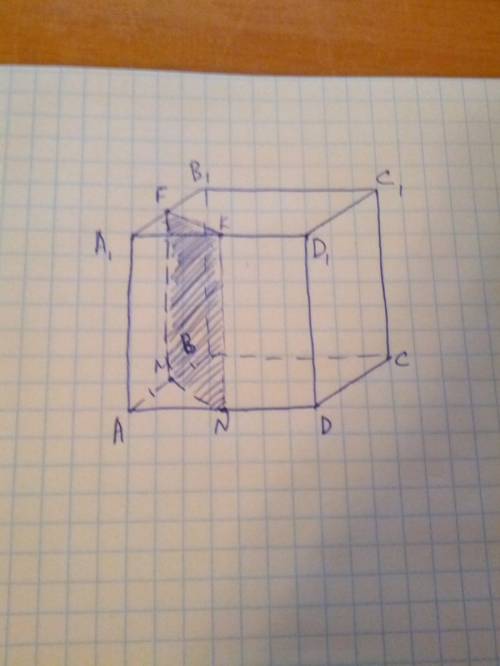
Построение сечения: Назовем искомую плоскость MNK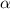 
. Плоскости ABC и A1B1C1 параллельны и пересечены плоскостью 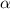, следовательно, линии пересечения параллельны. Значит, 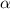пересекает А1В1С1 по прямой КF, параллельной MN. Значит, F - середина А1В1. Осталось соединить KF, FM, MN, NK. Искомое сечение - FKNM.
Доказательство: В треугольнике ABD MN-средняя линия, MN || BD. Т.к MN лежит в плоскости сечения MNK, а BD параллельна прямой MN, лежащей в плоскости сечения, ВD параллельна плоскости MNK, что и требовалось доказать.
Объяснение:
При пересечении двух хорд в одной точке произведение двух частей одной хорды равно произведению частей второй хорды.Для удобства Назовём хорды и точку их пересечения.Пусть Хорда АВ пересекается с хордой ТМ в точке К,тогда по теореме АК*КВ=ТК*КМ Тогда 2*9=ТК*КМ
Пусть ТК- равен х см ,тогда КМ=х+3.
Составляем уравнение 2*9=х*(х+3) ;18=х²+3х х²+3х-18=0
х²+3х-18=0
По теореме Виета
х1+х2=-3 х1=3
х1*х2=-18 х2= -6 Значение -6 нам не подходит,так как длина не может быть отрицательной .Поэтому ТК=3 см,тогда КМ=3+3= 6см
ответ: больший отрезок второй хорды равен 6 см