Рассмотрю три решения:
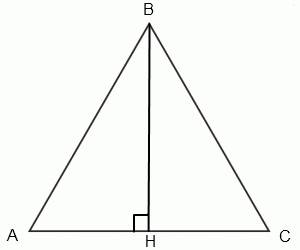
1) Пусть сторона AB = x, тогда AH = 0,5 * x, BH = 2 * (√3) ( по условию )
Тогда по теореме Пифагора: x ² = (0,5 * x) ² + (2 * (√3)) ²
x ² = (1/4 * x ²) + 4 * 3
x ² - (x ² / 4) = 12
(4 * x ² - x ²) / 4 = 12
3 * x ² = 48
x ² = 16
x = 4.
2) Треугольник ABH - прямоугольный, угол BAH = 60°.
sin 60° = BH / AB
AB = BH / sin 60°
AB = (2 * (√3)) / ((√3) / 2)
AB = 4.
3) Медианы в равностороннем треугольнике пересекаются в одной точке и делятся в соотношении 2:1 от вершины. 2/3 часть медианы будет являться радиусом описанной окружности. Значит R = (2 / 3) * 2 * (√3) = (4 * (√3)) / 3.
По теореме синусов:
2R = AB / sin 60°
(2 * 4 * (√3)) / 3 = AB / ((√3) / 2)
AB = (√3) / 2 * (8 * (√3) / 3)
AB = 4.
В прямоугольном треугольнике CНВ (<H=90°) угол НСВ (смежный с углом С треугольники АВС) равен 180°-120°=60°. Тогда <HBC=30° и катет СН=5 (половина гипотенузы СВ).
По Пифагору ВН=√(ВС²-НС²)=√(10²-5²)=√75см. Тогда в прямоугольном треугольнике ВКН гипотенуза НК - расстояние от точки К до прямой АС (перпендикуляр к АС по теореме о трех перпендикулярах).
По Пифагору НК=√(ВН²-ВК²)=√(75+150)=15см.
ответ: НК=15см.
2. 1) Точка М равноудалена от вершин треугольника,значит расстояния от основания перпендикуляра, опущенного из этой точки на плоскость АВС также равны. Следовательно, проекция Н точки М на плоскость АВС находится в середине гипотенузы АВ треугольника АВС и отрезок МН, принадлежащий плоскости АМВ, перпендикулярен плоскости АВС.Следовательно, плоскость АМВ перпендикулярна плоскости АВС, что и требовалось доказать.
2) Угол между плоскостями - двугранный угол - измеряется линейным углом, то есть углом, образованным пересечением двугранного угла с плоскостью, перпендикулярной к его ребру.Проведем плоскость МНР перпендикулярно ребру СВ двугранного угла между плоскостями АВС и СМВ. Для этого опустим перпендикуляр НР на прямую СВ и соединим точки М и Р. В прямоугольном треугольнике МРН <MPH - искомый угол, тангенс которого равен отношению МН/НР.
Гипотенуза АВ=4√2см (по Пифагору). Тогда СН=НВ=АН=2√2см.
НР- высота в равнобедренном треугольнике СНВ и НР=СН*НВ/СВ (свойство). НР=(2√2)*(2√2)/4=2см.
Tgα=МН/НР=2√3/2=√3. α=arctg√3 = 60°.
ответ: угол равен 60°.
3) Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость. Значит искомый угол - угол МСН, тангенс которого равен отношению МН/СН или tgβ=2√3/2√2 =√1,5. Угол β=arctg√1,5 ≈ 50,5°
Или так: по Пифагору МС=√(МН²+СН²)=√20=2√5см.
Тогда Sinβ = МН/МС=2√3/2√5 =√0,6. β=arcsin0,77 ≈ 50,5°.
ответ: угол равен arcsin√0,6 ≈ 50,5°.
3***. Расстояние от середины стороны АВ до плоскости ВМС - это перпендикуляр НТ из прямого угла МНР (точка Н совпадает с точкой Е) к гипотенузе МР треугольника МРН. по свойству он равен
НТ=МН*НР/МР. МР=√(МН²+НР²)=√(12+4)=4. Тогда НТ=2√3*2/4=√3.
ответ: расстояние равно √3.