1.Наибольшая высота в 3 см проведена к наименьшей стороне 16см, площадь равна половине произведения этой стороны на высоту. т.е. 3*16/2=24/см²/
2.Эта же площадь 24см² может быть посчитана, если его наименьшая высота будет проведена к наибольшей стороне, значит, деля две известные площади 2*24 на наибольшую сторону 24см, получим наименьшую высоту. 2*24/24=2/см/
3. Использовали формулу площади S=a*h/2, где S - площадь треугольника, a - сторона треугольника, в п.1 наименьшая, в п.2 наибольшая, h - высота треугольника, в п.1 наибольшая, в п. 2 наименьшая.
ответ 2см
Объяснение:
Вектор -это направленное перемещение.
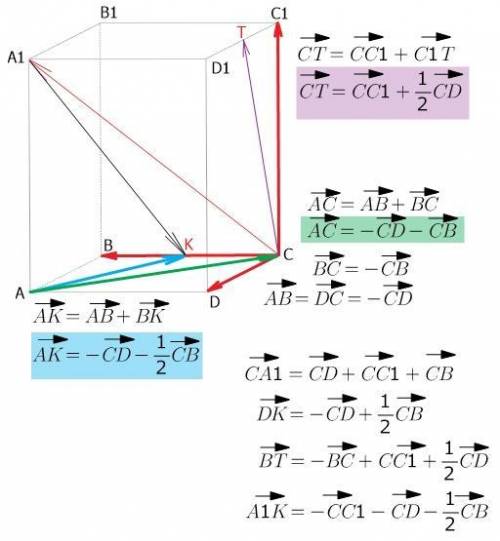
чтобы разложить векторы по указанным векторам, можно представлять, что "как будто вы вышли из вершины А и идете по ребрам призмы в вершину С и записываете свой путь"...
из точки А могу "пройти" в точку В (это вектор АВ); из В могу "пройти" в точку С (это вектор ВС)...
но перемещение из А в В (вектор АВ) по длине в точности равно
перемещению из С в D (вектору CD), только направление в другую сторону... направление "показывает" знак "минус"
вектор АВ = вектору DC
вектор DC = "минус" вектор CD
а)8+2а
б)а и (180°-а)°
в) Р=22, углы 60° и 120°
Объяснение:
а) Так как у ∆ АВН катет напротив угла 30° равен 2 то гипотенуза ( в два раза больше) равна 4. Периметр равен 2 (ВС+АВ) ( по определению противоположные стороны равны)
б)Так как у ∆ЕКР высота является медианой он равнобедренный (свойство) тогда угол КРЕ = углу КЕР= углу М = а (свойство параллелограмма) и односторонний ему равен (180°- а)
в)∆QRN — равносторонний так как ST=QR(по определению параллелограмма)=4 ( что равно QN) тогда угол Q = 60° = углу S и односторонний ему угол Т = 180°-60°=120°
Розв'язання
Объяснение:
Найбільша висота - висота, проведена до найменшої сторони (і навпаки).
Нехай найбільша висота - h. Вона проведена до найменшої сторони - 16 см. По формулі площі трикутника:
S = ah/2
S = (16 * 3)/2 = 24
Площа трикутника - 24 см²
Нехай найменша сторона -h'. Вона проведена до сторони 24 см. Тоді:
S = (24 * h')/2
24 = (24 * h')/2 = h' * 12
h' = 24/12 = 2
h' = 2 см