~ (приблизительно равно) 12 324,5
Объяснение:
Я использовал таблицу Брадиса что бы найти значения косинуса и тангенса 45 градусов (дробь корень из 2/2 это 0,7071 то есть корень из двух пополам)
Так как нам известен прямой угол 90 градусов и два угла при основании 45 градусов, то мы можем найти неизвестный катет: гипотенуза умноженная на синус прилежащего угла. Второй неизвестный катет можно найти так: известный катет умножить на тангенс противолежащего угла.
Затем площадь можно найти по формуле Герона, согласно которой площадь треугольника равна корню из произведения разностей полупериметра треугольника и каждой из его сторон на полупериметр.
Зачастую задачи на решения треугольников имеют приблизительный ответ.


BC=8, AC=8
Объяснение:
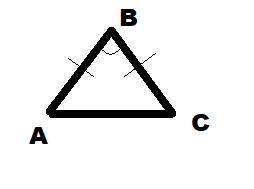
В треугольнике АВС стороны АВ и ВС равны, значит, этот треугольник равнобедренный, причем АС - основание. В равнобедренном треугольнике углы при основании равны. Значит, угол А равен углу С.
В треугольнике сумма всех углов равна 180 градусов. Поскольку угол В равен 60 градусов, то на углы А и С остается 120 градусов, а раз они равны, то каждый из них равен 120/2=60 градусов. Получаем, что в треугольнике все углы равны 60 градусов, а значит, что этот треугольник равносторонний, т.е. все стороны равны между собой и равны 8.
Обозначим пирамиду АВСS. S -вершина пирамиды, из вершины опустим на основание перпендикуляр SO. Точка О-в правильном треугольнике центр вписанной и описанной окружности. Обозначим середину SO точкой М, а середину апофемы SД-точкой К. Тогда в треугольнике ДSО-средняя линия КМ. Отсюда ДО=2*КМ=2 корня из 3. ДО=r-это радиус вписанной окружности. Треугольник ДSО- прямоугольный, проти угла в 30 градусо лежит катет вдвое меньший гипотенузы, значит апофема SД=2*ДО=4 корня из 3. Периметр правильного треугольника равен Р=6*(корень из 3)*r=6*(корень из 3)*(2 корня из 3)=36. Тогда площадь боковой поверхности равна Sбок. =1/2*Р*SД=1/2*36*(4 корня из 3)=72 корня из 3.