Т.к. трапеция описана около окружности, то сумма ее боковых сторон равна сумме оснований 4+36=40/см/. А поскольку боковые стороны у трапеции равны, то каждая по 40/2=20/см/, проведем из вершин тупых углов высоты, отрезок большего основания, который отсекает высота, образует треугольник вместе с боковой стороной, и равен полуразности оснований, т.е. (36-4)/2=16(см), а боковая сторона 20 см, тогда высота трапеции равна √(20²-16²)=12/см/, радиус равен половине высоты, т.е. 6см.
Решить данную задачу в 7 классе невозможно, поскольку она решается через теорему синусов, а это 9 класс! Возможно было бы решить задачу, если бы ∠BAD равнялся 115°, либо ∠BCF равнялся 55°. Тогда бы мы доказали, что ΔABC - равнобедренный и указали бы, что сторона AB равняется 5 см ( по свойству).
Что поделаешь: рассмотрим решение через теорему синусов.
Вертикальные углы равны.
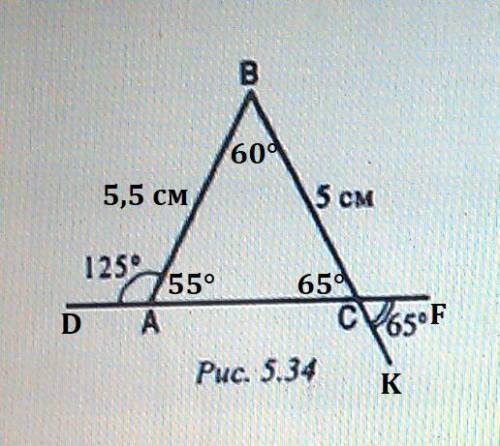
⇒ ∠FCK=∠BCA=65°, так как они вертикальные.
Сумма смежных углов равна 180°.
⇒ ∠BAD+∠BAC=180°, так как они смежные ⇒ ∠BAC=180°-125°=55°.
Сумма углов треугольника равна 180°.
⇒ ∠ABC=180°-(55°+65°)=180°-120°=60°.
Теорема синусов: Стороны треугольника пропорциональны синусам противолежащих углов.
AB:sinBCA=AC:sinABC=BC:sinBAC ⇒
AB=BC*((sinBCA)/(sinBAC)) ⇒
AB=5*((sin65°)/(sin55°))≈5*(0,906/0,819)≈5,5 (см).
ответ: AB≈5,5 (см).
начертим отрезок с заданными координатами его концов (x1; y1) и (x2; y2). На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.
Вычислим длину данных проекций. Итак, на ось Y длина проекции равна y2-y1, а на ось Х длина проекции равна x2-x1. Применим теорему Пифагора: |AB|² = (y2 - y1)² + (x2 - x1)². В данном случае |AB| является длиной отрезка.
Решение
Объяснение:
Радиус вписанной в равнобедренную трапецию окружности равен половине ее высоты.
Назовем трапецию ABCD (BC ║ AB), проведем высоту CK к точке K.
Вписанная окружность прикасается к серединам сторон.
Обозначим эти середины: M (AB), L (BC), N (CD), F (AD).
Касательные, проведенные с одной точки равны:
BM = BL = CL = CN = 2
AM = AF = DF = DN = 18
CD = 2 + 18 = 20
Рассмотрим ΔCKD:
∠CKD = 90° (CK - высота)
KD = (AD - BC) / 2 = (36 - 4) / 2 = 32/2 = 16 (по свойству равнобедренной трапеции)
KD = 16
По теореме Пифагора:
CK² = CD² - KD²
CK = √(400 - 256) = √144 = 12
CK = 12
r = CK/2 = 12/2 = 6
r = 6 см