Рассмотрим ΔКДА: ∠ДКА = 60°, ∠КАД = 90°, т.к. ДА высота ⇒
∠КДА = 180°-(60°+90°) = 30°
Т.к. ΔКДА прямоугольный, то в нем катет, лежащий против угло в 30° равен половине гипотенузы. Катет КА нам дан и равен 5 см, значит гипотенуза КД = 10 см
По т.Пифагора в ΔКДА КД² = КА² + АД² ⇒ АД² = КД²-КА²
в ΔАДС ДС² = ДА² + АС² подставляем АД²
ДС² = КД²-КА²+АС² = 100-25+46 = 121
ДС = 11 см
Объяснение:
а) Проекция точки S на плоскость основания это точка O — центр основания. Центр правильного треугольника является точкой пересечения его медиан, поэтому . Прямая проецируется на плоскость основания и прямую Поэтому проекция точки — точка — лежит на отрезке M — середина AS, поэтому ее проекция — это середина отрезка AO. Таким образом, проекции точек S и M на плоскость основания делят высоту AN треугольника ABC на три равные части.
б) Прямая проектируется на плоскость основания в прямую Поэтому проекция точки — точка — лежит на отрезке Значит, прямая является проекцией прямой следовательно, угол — искомый. Заметим, что где — центр основания, значит, — средняя линия треугольника а поэтому — середина
Тогда
и
Из прямоугольного треугольника находим:
Из прямоугольного треугольника находим:
Значит, искомый угол равен
ответ:arctg 10/21
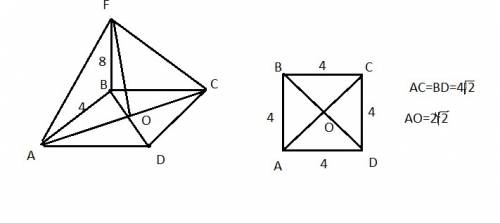
11
Объяснение:
Подробное объяснение на фото