Сделаем рисунок.
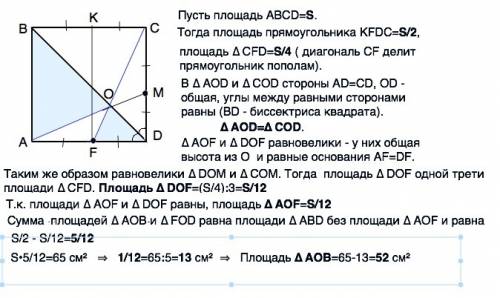
Пусть площадь АВСD=S.
Тогда площадь прямоугольника KFDC=S/2,
площадь ∆ СFD=S/4 ( диагональ CF делит прямоугольник пополам).
В ∆ АОD и ∆ СОD стороны АD=СD, ОD - общая, углы между равными сторонами равны (BD - биссектриса квадрата).
∆ АОD=∆ СОD.
∆ АОF и ∆ DOF равновелики - у них общая высота из О и равные основания АF=DF.
Таким же образом равновелики ∆ DОМ и ∆ СОМ. Тогда площадь ∆ DОF одной трети площади ∆ СFD. Площадь ∆ DOF=(S/4):3=S/12
Т.к. площади ∆ АОF и ∆ DOF равны, площадь ∆ АОF=S/12
Сумма площадей ∆ АОВ и ∆FOD равна
площади ∆ ABD без площади ∆ АОF и равна S/2-S/12=5/12
По условию эта сумма S•5/12=65 см²
1/12=65:5=13 см²
Площадь ∆ АОВ=65-13=52 см²
Р = 20 +16 +12=48 (см), S = 0,5·BC·AC = 0,5·16·12 = 96(cм²).
2) Р = 3·a = 12√3
a = 12√3/3 = 4√3.
a = R√3
4√3 =R√3
R = 4, r = R/2=4/2=2